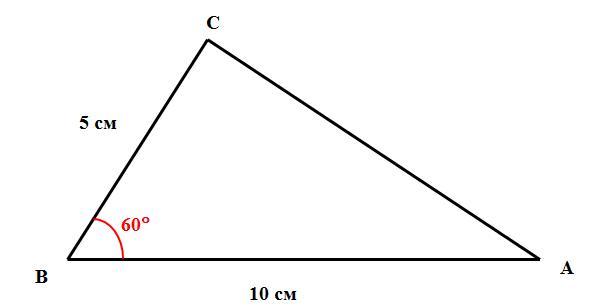
Дан треугольник ABC. Если AB = 10 см, BC = 5 см и ∠B =60°, то найди длину стороны AC.
Округли ответ до целого числа.
orjabinina:
т косинусов
"Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними" , то
АС²=АВ²+ВС²-2*АВ*ВС*cosA,
АС²=10²+5²-2*10*5*cos60,.......АС²=10²+5²-2*10*5*0,5=...............
АС²=АВ²+ВС²-2*АВ*ВС*cosA,
АС²=10²+5²-2*10*5*cos60,.......АС²=10²+5²-2*10*5*0,5=...............
Ответы
Ответ дал:
5
Ответ:
AC = 5·√3 см
Объяснение:
Дано (см. рисунок):
ΔABC
AB = 10 см
BC = 5 см
∠B =60°
Найти: AC.
Решение. Задача для применения теорему косинусов:
AC² = AB² + BC² - 2·AB·BC·cos∠B.
Подставим известные значения:
AC² = 10² + 5² - 2·10·5·cos60° = 100 + 25 - 2·50·0,5 = 125 - 50 = 75 см².
Отсюда
AC = √(75) = √(25·3) = 5·√3 см.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад