35 баллов., решить логарифмические уравнения используя свойства логарифма.
ПОШАГОВО, С ФОТО.
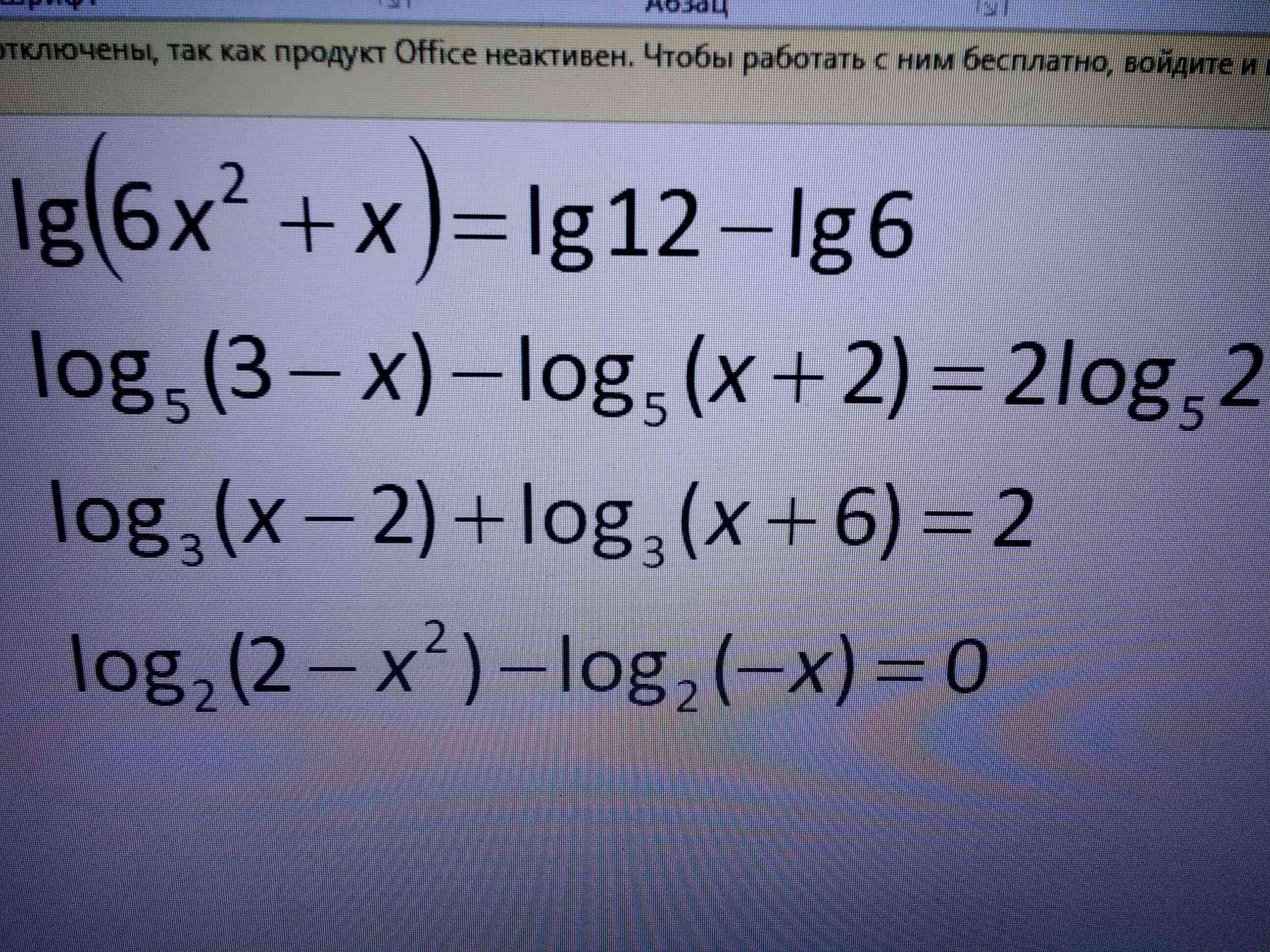
Ответы
1)
При решении логарифмических уравнений всегда сначала нужно находить область определения. Аргумент логарифма всегда должен быть положительным, а основание - не только положительным, но и неравным единице. С основаниями всё в порядке, поскольку - это логарифм с основанием 10. Теперь с аргументами. 12 и 6 положительны, а вот у логарифма в левой части уравнения в аргументе находится переменная, а потому область определения является решением неравенства:
Нули: .
+ - +
--------------------о---------------------------о-----------------------> x
Таким образом, запишем область определения функции:
По свойству логарифма: , тогда для нашего случая:
Так как основания логарифмов одинаковые, мы можем приравнять аргументы.
Оба корня входят в выведенную нами область определения, а потому они оба являются решениями уравнения.
Ответ: .
2)
Для нахождения области определения проверяем каждое расписанное мной сверху свойство для каждого логарифма. В итоге должно получиться:
Теперь воспользуемся двумя свойствами логарифмов. Первое мы применяли в прошлом уравнении, а второе: .
По основному свойству пропорции:
Корень входит в область определения, а значит, является решением уравнения.
Ответ: -1.
3)
Уже по стандарту находим область определения.
Воспользуемся свойством логарифма: . Двойку в правой части нам нужно заменить на тождественный ей логарифм по основанию 3, таким будет
.
По теореме Виета:
А теперь внимание, то, зачем мы искали область определения. Напомню, она у нас была . Найденный нами корень -7 в этот промежуток не входит, а потому решением уравнения НЕ ЯВЛЯЕТСЯ. С корнем 3 же всё нормально, а значит, уравнение имеет одно решение.
Ответ: 3.
4)
Область определения:
Верхнее неравенство решим отдельно.
Нули: .
- + -
-----------------------о---------------------------о-----------------------> x
0 - это логарифм с аргументом 1, при этом основание может быть любым допустимым. Например, 2, как в нашем случае: . Пользуемся тем же свойством.
Откуда получаем, что:
По теореме Виета:
Опять сравниваем с областью определения. Легко заметить, что 2 в неё не входит, а значит, НЕ ЯВЛЯЕТСЯ РЕШЕНИЕМ. А -1 входит туда, поэтому уравнение имеет одно решение.
Ответ: -1.
log(2-x²) - log(-x) = 0
log(2-x²) = log(-x)
2-x² = -x