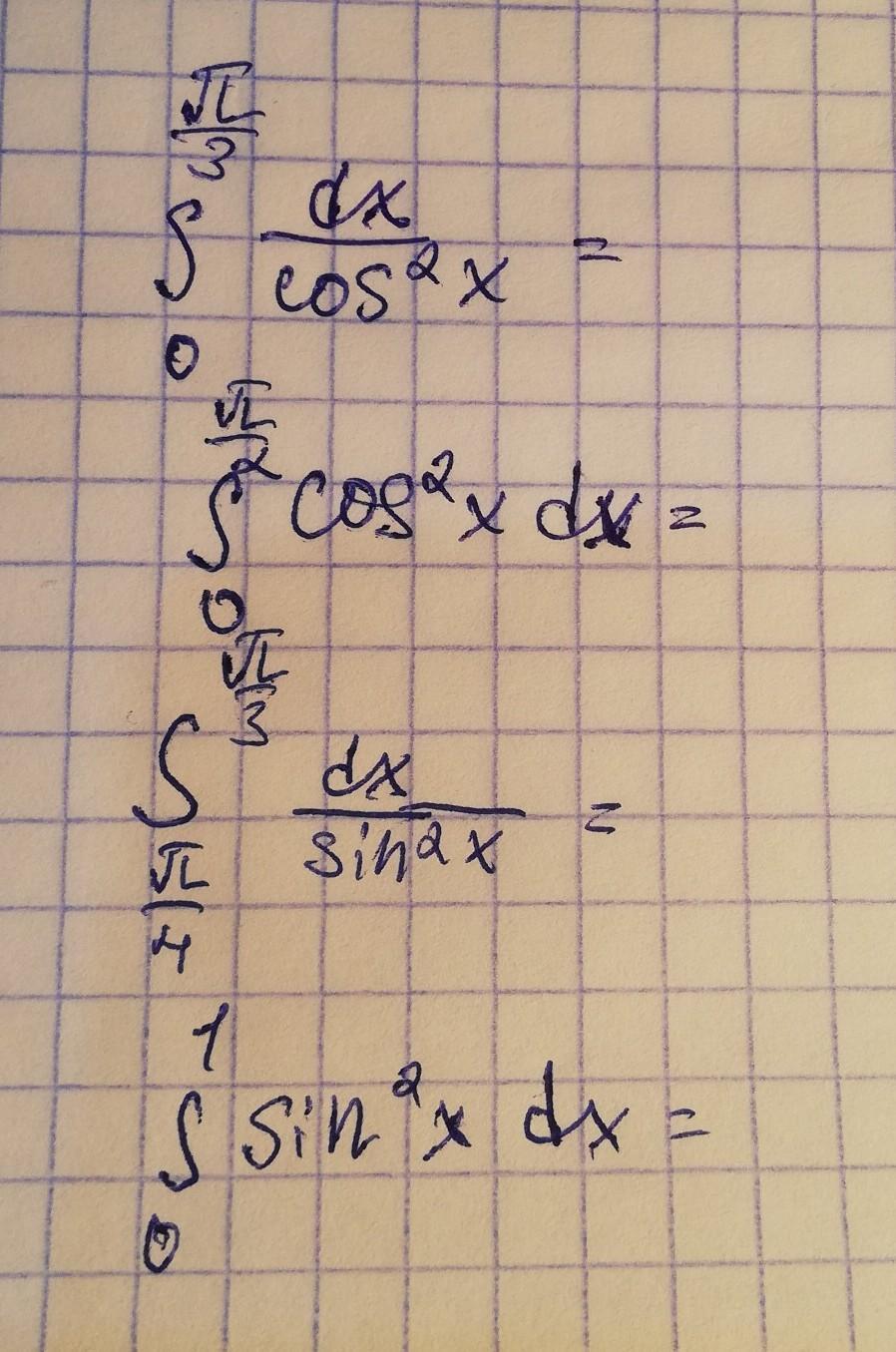Ответы
Ответ дал:
1
Ответ:
1.
2.
3.
4.
Miroslava227:
существует формула понижения степени
sin^2(x) =(1-cos(2x))/2
и у косинуса есть
можно загуглить
потом выносим 1/2 за знак интеграла и получаем (1-cos2x)dx
делим на 2 интеграла 1*dx и cos2xdx
первый равен х
чтобы решить второй, добавляем двойку в дифференциал, а для этого распишем 1 как 1/2 * 2
то есть получаем 1/2 cos2xd(2x) и интегрируем как sin2x
спасибо огромное
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад