Question

Высота равнобокой трапеции равна 109 см, а её диагонали перпендику-лярны. Найдите боковую сторону трапеции, если её периметр равен 48 см.

Answer 1

Ответ:

13,1 см

Объяснение:

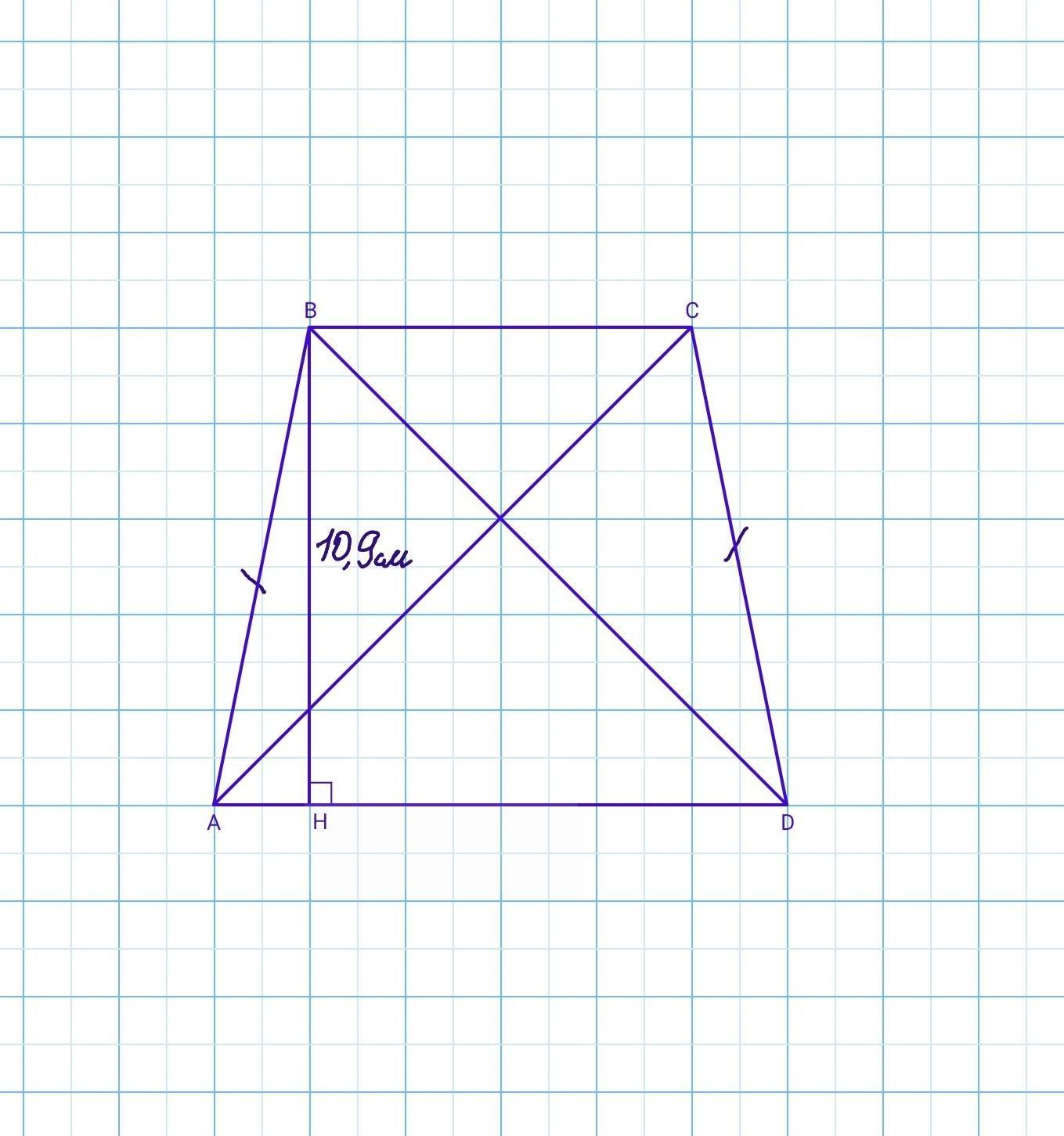
Дано: ABCD - трапеция. АВ=CD (так как боковые стороны равнобокой трапеции равны). BH - высота. ВН⟂AD. BH = 10,9 см. Р(ABCD) = 48 см

Найти: АВ -?

• Если в равнобедренной трапеции диагонали перпендикулярны, то высота трапеции равна полусумме оснований:

$BH = \dfrac{1}{2} (BC + AD)$

ВС + AD = 2BH

Периметр трапеции - это сумма всех её сторон: Р = АВ + BC + CD + AD.

Так как АВ=CD, а ВС + AD = 2BH, то Р = 2АВ + 2ВН.

По условию задачи периметр равен 48 см, а ВН=10,9 см:

2АВ + 2×10,9 = 48

АВ + 10,9 = 24

АВ = 24 - 10,9 = 13,1 см

Боковая сторона равнобокой трапеции равна 13,1 см