Упростить выражение: -2sinA×cosA-sin^3A-cos^3A-3sin^2A×cosA+3sinA×cos^2A/sinA-cosA
Приложения:
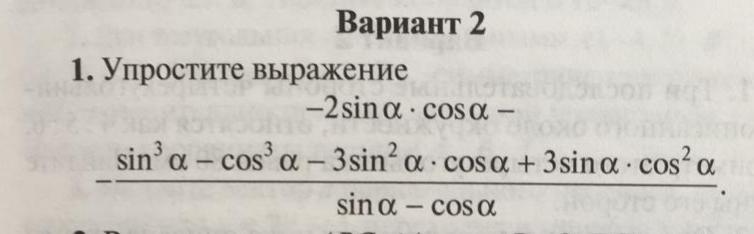
orjabinina:
ВЫ НЕВЕРНО НАПИСАЛИ ЗНАКИ. проверьте. Там формула суммы кубов должна получиться.
Ответы
Ответ дал:
2
Объяснение:
Преобразуем числитель дроби
sin³α-cos³α-3sin²α×cosα+3sinα×cos²α=
=sin³α -3sin²α×cosα+3sinα×cos²α-cos³α=( по формуле куб разности )=
=(sinα -cosα)³ . Тогда дробь примет вид
(sinα -cosα)²=sin²α -2sinα*cosα+cos²α = ( применяя основное тригонометрическое тождество)= 1 -2sinα*cosα.
Учтем выражение стоящее перед дробью
-2sinα*cosα - (1 -2sinα*cosα)= -2sinα*cosα-1 + 2sinα*cosα = -1
Спасибо большое! Очень помогли!
обращайтесь
чуть исправила
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад