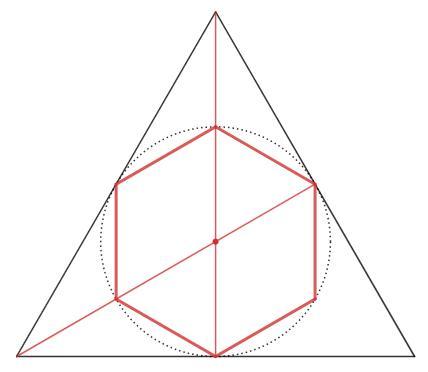
ДАБ 18 БАЛОВ!!! Около окружности описан равносторонний треугольник и в нее вписан правильный шестиугольник . найдите стороны шестиугольника . если сторона треугольника 12м. ОТВЕТ ДОЛЖЕН БЫТЬ 4м МНЕ НУЖНО ПОЛНОЕ РЕШЕНИЕ ПОЧЕМУ ОТВЕТ 4?пжжжжж помогите
Ответы
Объяснение:
R описанный
r вписанный окружности
это для правильного треугольника,четырёхугольника и шестиугольника

Центр вписанной окружности - точка пересечения биссектрис.
В равностороннем треугольнике биссектрисы являются медианами и высотами.
Высота равностороннего треугольника по теореме Пифагора:
h =√(a^2 -(a/2)^2) =a √3/2
Медианы точкой пересечения делятся в отношении 2:1 от вершины.
Радиус вписанной окружности равностороннего треугольника:
r =1/3 h =a √3/6
Вершины правильного шестиугольника делят описанную окружность на шесть равных дуг, 360/6 =60.
Радиусы образуют со стороной шестиугольника равносторонний треугольник (равнобедренный с углом 60).
Следовательно, сторона правильного шестиугольника равна радиусу описанной окружности:
x =a √3/6 =12 √3/6 =2√3