Ответы
Ответ дал:
1
Ответ:
13см
Объяснение:
Площадь ромба равна половине произведения его диагоналей:
S = (AC · BD) / 2.
BD=12х, АС=5х, тогда:
BD=12х=12*2=24cм, АС=5х=5*2=10см
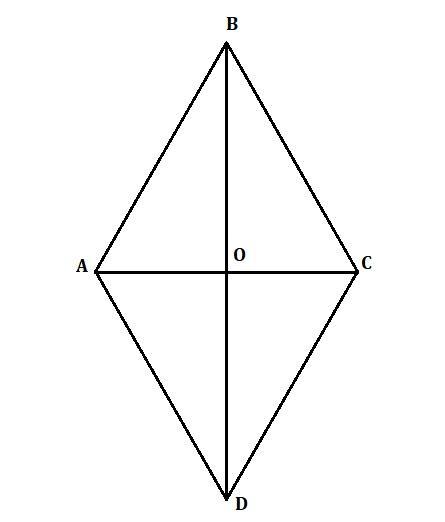
Так как диагонали ромба перпендикулярны друг другу, то рассмотрим прямоугольный треугольник АВО(∠0=90°).
Диагонали ромба точкой пересечения делятся пополам ⇒ АО=АС/2=10/2=5см,
ВО=ВD/2=24/2=12см.
По теореме Пифагора найдём гипотенузу АВ, которая является стороной ромба (у ромба все стороны равны):
Сторона ромба АВ = 13см
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9.14,2