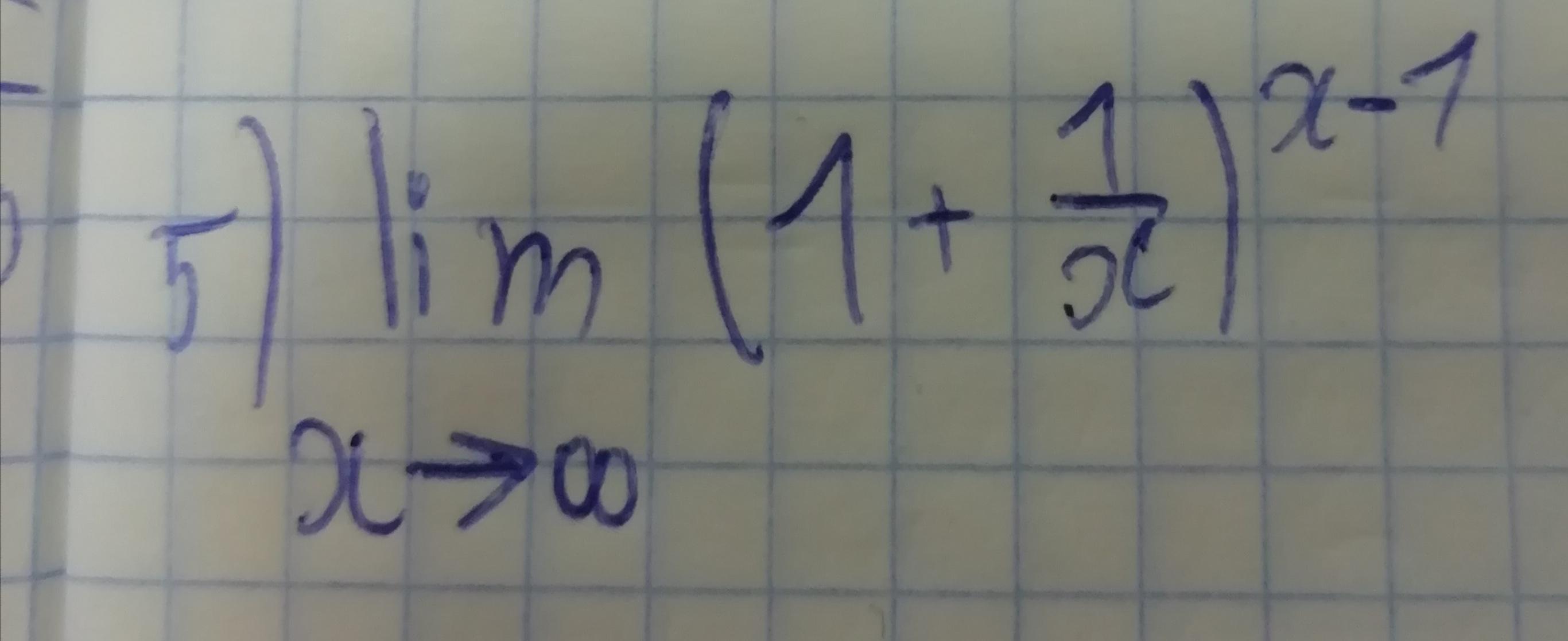Ответы
Ответ дал:
0
Ответ:
e
Пошаговое объяснение:
2ой замечательный предел:
делим во втором пределе на x и знаменатель и числитель.
1/x при x->+∞=0
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад