У прямокутну трапецию з периметром 242 см вписано коло радіус якого = 30см. Знайдіть відрізки більшої бічної сторони , трапеції на які її ділить точка дотику кола. якщо різниця цих відрізків = 11см
ДАЮ 100 БАЛЛОВ ПОМОГИТЕ
orjabinina:
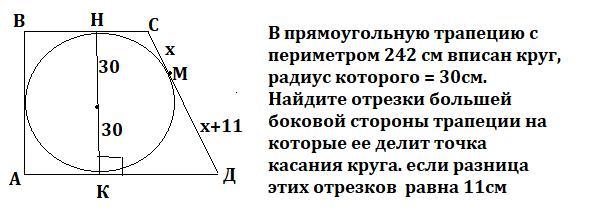
В прямоугольную трапецию с периметром 242 см вписан круг, радиус которого = 30см. Найдите отрезки большей боковой стороны трапеции на которые ее делит точка касания круга. если разница этих отрезков = 11см
Ответы
Ответ дал:
1
В прямоугольную трапецию с периметром 242 см вписан круг, радиус которого = 30см. Найдите отрезки большей боковой стороны трапеции на которые ее делит точка касания круга. если разница этих отрезков равна 11см
Объяснение:
Большая боковая сторона это СД
Если четырёхугольник описан около окружности, то суммы длин его противоположных сторон равны⇒АВ+СД=ВС+АД=242:2=121 (см).
Радиус, проведенный в точку касания перпендикулярен касательной ⇒ R=НК=АВ=30*2=60(см).
Значит АВ+СД=121 , 60+СД=121 , СД=61 см.
Пусть меньший отрезок стороны СД будет х см, тогда больший отрезок стороны СД= будет х+11, а из сумма 61 см. Составим уравнение : х+х+11=61 , х=25см
Меньший отрезок 25 см, больший отрезок 25+11=36 (см)
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад