Question

Точка P делит хорду MK окружности на два отрезка длиной 8см и 12см. Найдите расстояние от точки P до центра окружности, если ее радиус равен 11см.

Answer 1

Ответ:

ОР=5см

Объяснение:

Дано:

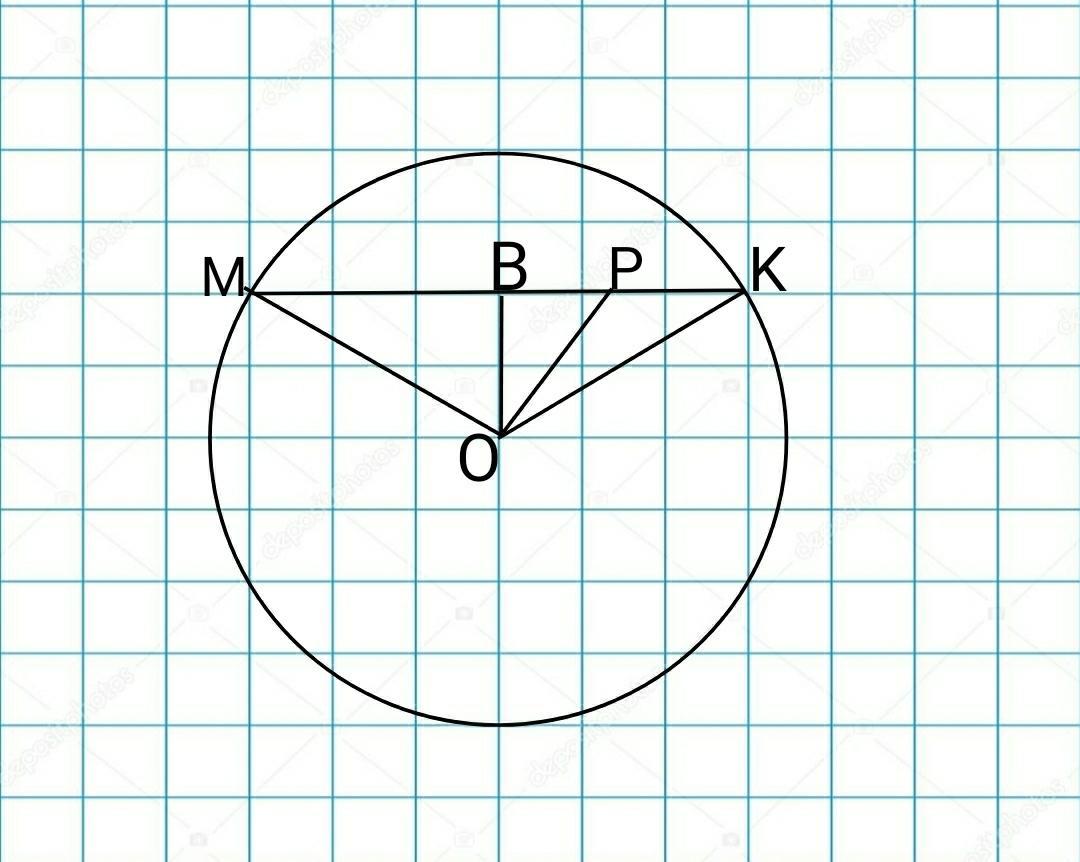
О- центр окружности.

МК- хорда

МР=12см

РК=8см

МО=ОК=11см радиус окружности

ОР=?

Решение

МК=МР+РК=12+8=20см.

Проведём высоту ОВ в ∆МОК

Высота ОВ- медиана, так как ∆МОК- равнобедренный.

МВ=ВК=МК:2=20:2=10см

∆МОВ- прямоугольный треугольник.

По теореме Пифагора найдем

ОВ=√(МО²-МВ²)=√(11²-10²)=√(121-100)=

=√21 см

ВР=ВК-РК=10-8=2см

∆ОВР- прямоугольный треугольник.

По теореме Пифагора

ОР=√(ОВ²+ВР²)=√((√21)²+2²)=√(21+4)=√25=

=5см