производная сложной функции.найти по формуле u'v-v'u/u^2
Приложения:
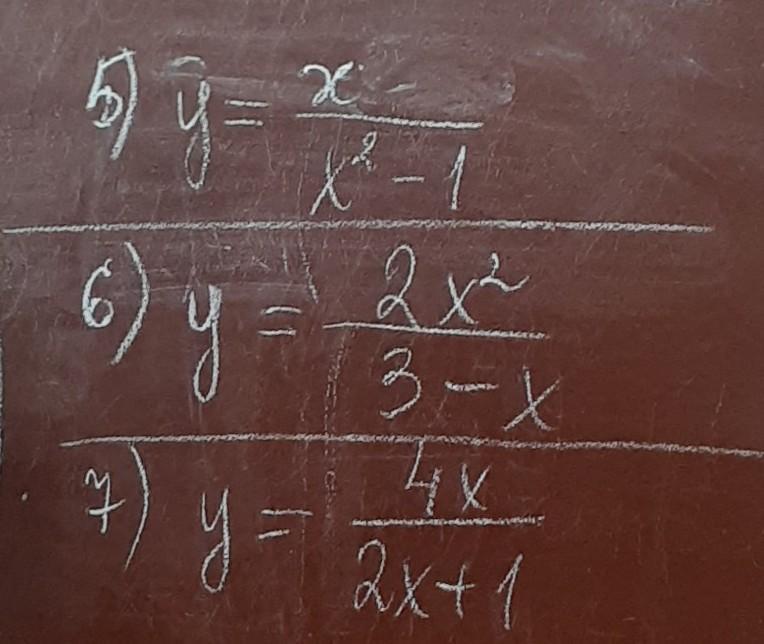
niko151983:
Это производная частного
Ответы
Ответ дал:
1
Ответ:
5.
6.
7.
помогите мне пожалуйста!!
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад