Докажите, что точка лежащая на биссектрисе угла AOB находится на одинаковом расстоянии от прямых AO и BO
Ответы
Ответ дал:
4
Ответ:
Решение:
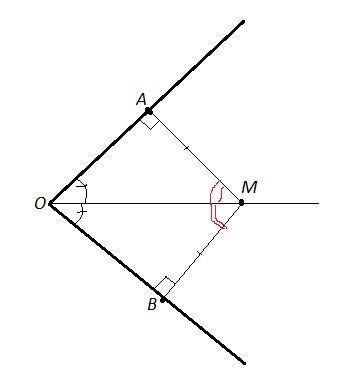
Расстояние от точки М (на биссектрисе) до стороны угла измеряется длиной перпендикуляра, опущенного из этой точки на сторону угла.
∠МАО=∠МВО=90°
∠АОМ=∠ВОМ, так как ОМ- биссектриса.
Соответственно
∠АМО=90°-∠АОМ
∠ВМО=90°-∠ВОМ- как острые углы прямоугольного треугольника
Можем утверждать, что ∠АМО=∠ВМО,
По второму признаку равенства треугольников: сторона и два прилежащие к не угла( ОМ- общая, ∠АМО=∠ВМО и ∠АОМ=∠ВОМ)
ΔАОМ=ΔВОМ. В равных треугольниках против соответственно равных углов лежат равные стороны, отсюда МА=МВ, что и требовалось доказать
Приложения:
Аноним:
Помогите пожалуйста https://znanija.com/task/42096487
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад