Question

Срочно!!! 25 баллов!!

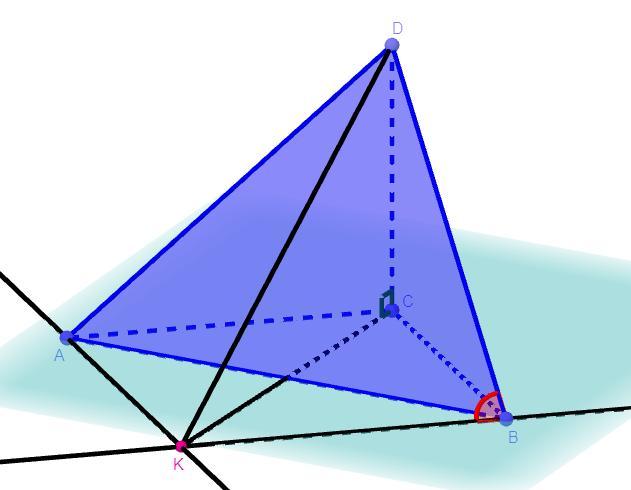
Ребро DС тетраэдра DABC перпендикулярно плоскости АВС. Известно, что АВ=5 см, АС =7 см, ВС=DC= 4 Корня из 2 см. Найдите угол между прямыми BD и Ас.

Answer 1

Ответ:

$\boxed{\angle(BD,AC) = 60^{\circ}}$

Объяснение:

Дано: DABC - тетраэдр, AB = 5 см, AС = 7 см, BC = DC = $4\sqrt{2}$ см,

DC ⊥ ABC

Найти: $\angle(BD,AC)$ - ?

Решение: Если одна из двух прямых лежит в плоскости, а другая прямая пересекает эту плоскость в точке, которая не принадлежит первой прямой, то данные прямые скрещивающиеся, так как $AC \subset ABC$ и $(BD \cap ABC) \notin AC$, то прямые BD и AC -  cкрещивающиеся. По определению угол между скрещивающимися прямыми это угол между прямыми которые пересекаются и соответственно параллельны данным скрещивающимся прямым. Через точку B проведем прямую параллельную AC, аналогично через точку A проведем прямую параллельную BC. Пусть прямая проведенная через точку B и параллельная AC и прямая проведенная через точку A и параллельная BC пересекаются в точке K. Так как по построению BK║AC, то по определению угла между скрещивающимися прямыми $\angle(BD,AC) = \angle(BD,BK)$. Так как по определению прямая перпендикулярная к плоскости перпендикулярна к любой прямой лежащей в этой плоскости, то так как DC ⊥ ABC и (BC,CK) ⊂ ABC, то DC ⊥ (BC,CK).По теореме Пифагора для треугольника ΔDCB: $BD^{2} = DC^{2} + BC^{2} = (4\sqrt{2})^{2} + (4\sqrt{2})^{2} = 32 + 32 = 64$. По определению параллелограмма его противоположные стороны параллельны, тогда так как по построению AC║BK и BC║AK, то четырехугольник ABCK - параллелограмм. Так как ABCK - параллелограмм, то по свойствам параллелограмма его противоположные стороны равны, тогда AC = BK = 7 см, BC = AK = $4\sqrt{2}$ см. По тождеству параллелограмма(ABCK): $2(AC^{2} + BC^{2}) = CK^{2} + AB^{2} \Longrightarrow CK^{2} = 2(AC^{2} + BC^{2}) - AB^{2} =$

$= 2(7^{2} + (4\sqrt{2} )^{2}) - 5^{2} = 2 (49 + 32) - 25 = 2 \cdot 81 - 25 = 162 - 25 = 137$.

По теореме Пифагора для (DC ⊥ CK) треугольника ΔDCK: $KD^{2} = KC^{2} + DC^{2} = 137 + 32 = 169$. По теореме косинусов для треугольника ΔDKB: $BK^{2} + BD^{2} - 2 \cdot BK \cdot BD \cos \angle KBD = KD^{2} \Longrightarrow$

$\Longrightarrow \cos \angle KBD = \dfrac{BK^{2} + BD^{2} - KD^{2}}{2 \cdot BK \cdot BD} = \dfrac{7^{2} + 64 -169}{2 \cdot 7 \cdot 8} = \dfrac{49 + 64 - 169}{112} =$

$= \dfrac{49 + 64 - 169}{112} = - \dfrac{56}{112} = -0,5$. $\angle KBD = \arccos (\cos \angle KBD) = \arccos(-0,5) = \pi - \arccos(0,5) = 180^{\circ} - 60^{\circ} =$

$= 120^{\circ}$. По определению угол между прямыми принадлежит промежутку от 0° до 90° включительно. При пересечение прямых образуются два угла. Так как угол ∠KBD - это угол который образуется при пересечении прямых KB и BD, однако ∠KBD > 90°, поэтому угол $\angle(BD,BK)$ равен углу смежному с углом ∠KBD. По свойству смежных углов их сумма 180°, тогда $\angle(BD,BK) = 180^{\circ} - \angle KBD = 180^{\circ} - 120^{\circ} = 60^{\circ}$.

Так как $\angle(BD,AC) = \angle(BD,BK)$, то $\angle(BD,AC) = 60^{\circ}$.