пожалуйста, ОЧЕНЬ СРОЧНО!!
найдите наибольшее и наименьшее значение функции на отрезке [-1; 0,5]
(фото функции внизу)
решите, пожалуйста, но не кратко
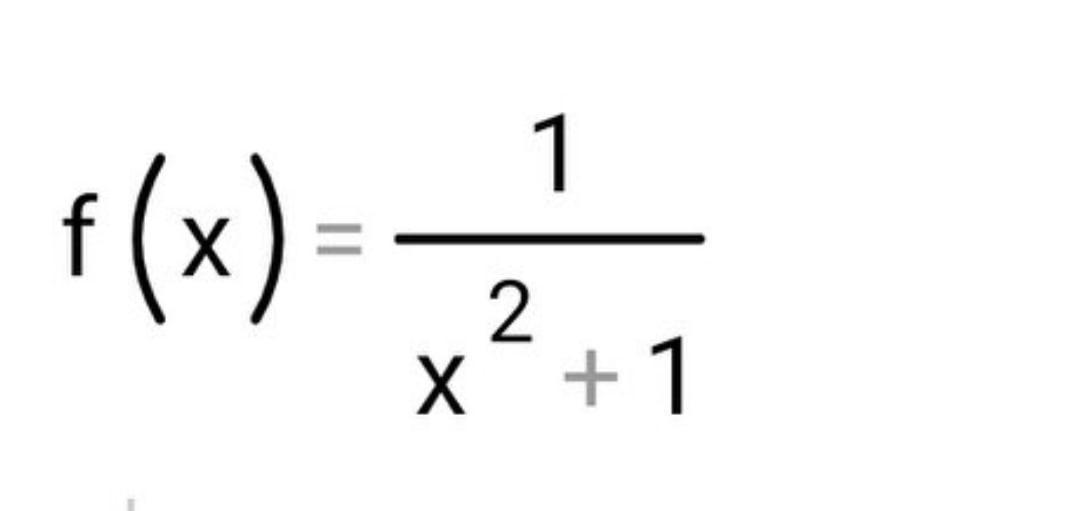
Ответы
Ответ:
Наименьшее значение 0,5 (при х=-1)
Наибольшее значение 1 (при х=0)
Объяснение:
Очевидно, что наибольшее и наименьшее значения функции совпадают с обратными к наименьшим и наибольшим (соответственно) значениям функции x^2+1
Наименьшее значение эта функция принимает при х=0 и это значение равно 1.
Значит у исходной функции это наибольшее значение.
при х больше 0 функция монотонно возрастает, при х меньше 0 монотонно убывает. Значит , сравнив значения на краях отрезка заключаем, что наибольшее значение достигается при х=-1 и равно 2.
Наименьшее значение исходной функции равно 1/2.
--------------------------------------
Примечание.
Конечно, можно использовать и стандартный ход с анализом производных. Однако, здесь функция строго положительная и 1/f(x) -выглядит особенно просто (симметричная порабола с минимумом в 0). Поэтому приведенное выше рассуждение представляется более простым и наглядным.