Ширина прямоугольника на 5 см меньше, чем длина. Периметр – 58 см. Найди площадь прямоугольника.
Составь уравнение, содержащее неизвестную x, согласно условиям задачи.
Ответ: (
+
+
) ∙
=
.
Площадь прямоугольника –
см2.
Приложения:
princessarujan01:
Спасибо у самое правильное у тебя
Спасибо большое
от души
Спс челу выши
Хахахаха
пасиб челу в комментах
lf cgc
да спс хотя спс звучит как слово спас тоьк а убираем и все
Ой.
фри фарчики
Ответы
Ответ дал:
1
Ответ:
Площадь прямоугольника - 204 см².
Пошаговое объяснение:
Периметр прямоугольника определяется по формуле:
где a- длина прямоугольника, b- ширина прямоугольника.
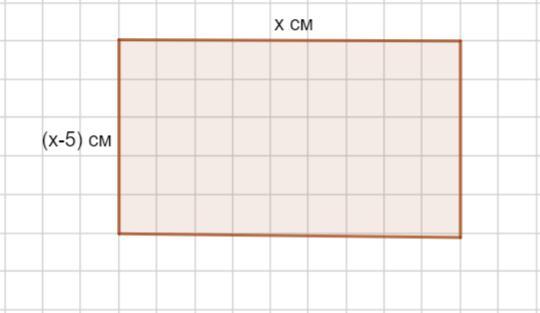
Пусть х см длина прямоугольника, а (х-5) см ширина прямоугольника.
Так как периметр прямоугольника равен 58 см, то составляем уравнение:
Значит, длина прямоугольника равна 17 см. Найдем ширину прямоугольника, если она на 5 см меньше длины.
(см)- ширина прямоугольника.
Для того чтобы найти площадь прямоугольника, надо длину умножить на ширину .
(см²)
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад