Question

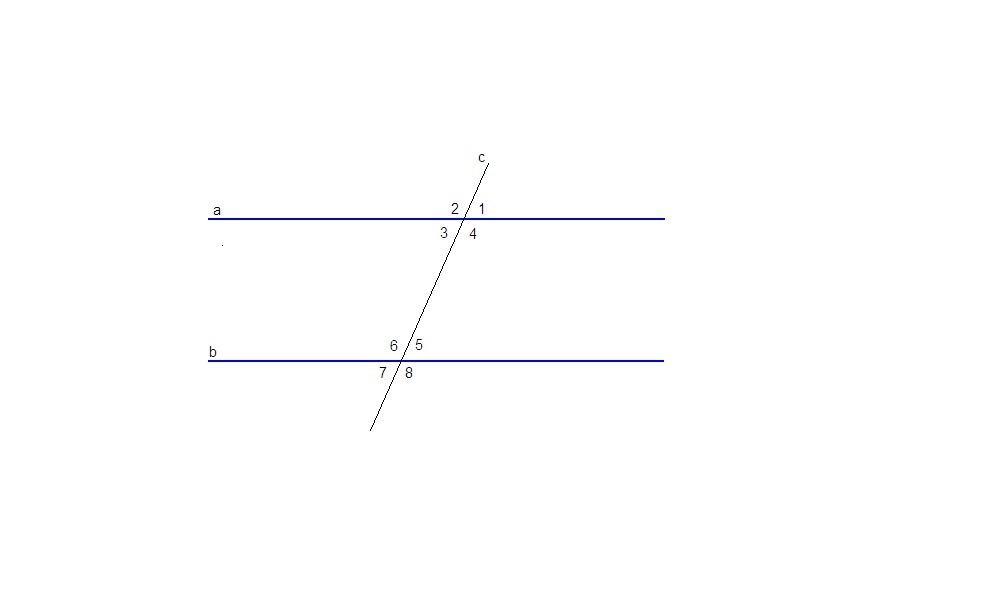
Найдите все углы образовавшиеся при пересечении двух параллельных прямых A и B секущей C ,если один из углов в 4 раз больше другого.

Answer 1

Объяснение  При пересечении параллельных прямых секущей образуется 8 углов двух величин:

соответственные углы

∠1 = ∠5

∠3 = ∠7,

а так как ∠1 = ∠3 как вертикальные, то

∠1 = ∠5 = ∠3 = ∠7 = х

и соответственные углы

∠2 = ∠6

∠4 = ∠8,

а так как ∠2 = ∠4, как вертикальные, то

∠2 = ∠6 = ∠4 = ∠8  = у

Сумма односторонних углов равна 180°, например

∠3 + ∠6 = 180°

Т. е. х + у =  180°.

 

Углы, о которых идет речь в задаче, не равны, значит их сумма 180°:

х - меньший угол, у = 5х

x  + 5x = 180°

6x = 180°

x = 30°

∠1 = ∠5 = ∠3 = ∠7 = 30°

у = 180° - 30° = 150°

∠2 = ∠6 = ∠4 = ∠8= 150°