Куб суммы и разности двух выражений. Урок 1
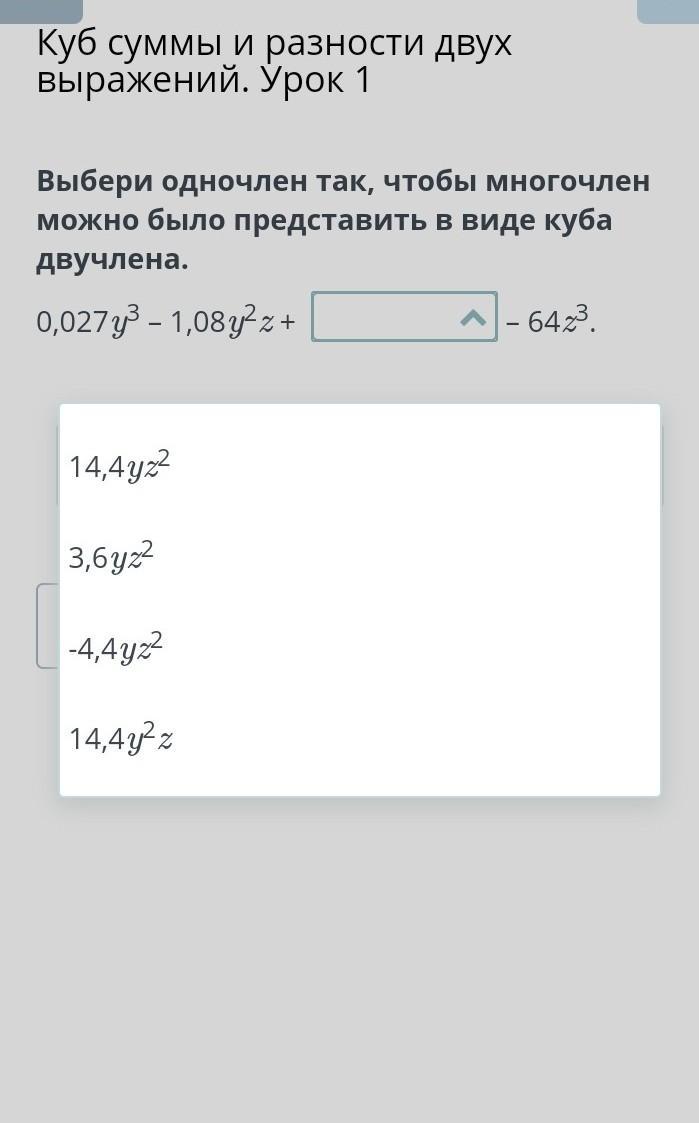
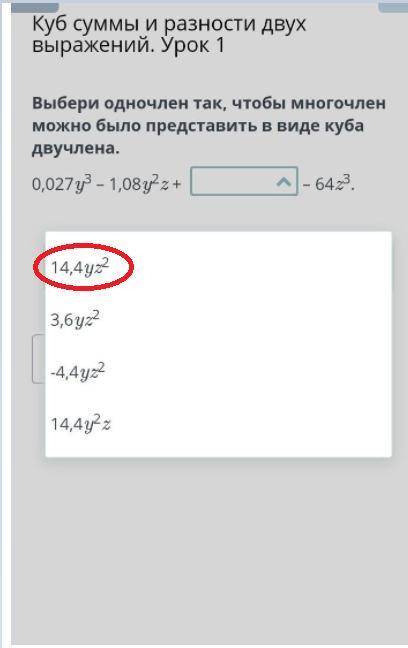
Выбери одночлен так, чтобы многочлен можно было представить в виде куба двучлена.
0,027y3 – 1,08y2z +
– 64z3.
Назад
Проверить
Приложения:
Ответы
Ответ дал:
3
Ответ:
Объяснение:
Воспользуемся формулой сокращенного умножения
Первое выражение представляет куб, тогда представим данное выражение в виде куба
Тогда
Рассмотрим последнее выражение, оно должно быть тоже кубом.
Значит,
Пропущенное выражение, согласно формуле будет
Тогда пропущено выражение
Приложения:
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
9 лет назад