Ответы
Ответ дал:
3
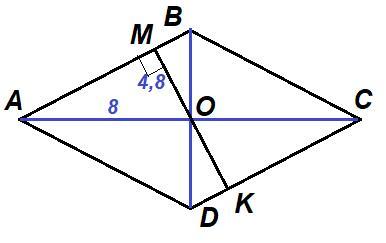
Дано: ABCD - ромб; AC = 16 см; h = 9,6 см.
Найти: S
Решение:
Диагонали ромба пересекаются под прямым углом и делятся точкой пересечения пополам:
AC⊥BD; AO = OC = 16 : 2 = 8 см.
Проведём высоту ромба MK через точку пересечения диагоналей O.
MK = h = 9,6 см
Прямоугольные треугольники OMB и OKD равны по равным вертикальным углам:
∠MOB = ∠KOD ⇒ ΔOMB = ΔOKD
⇒ OM = OK = MK : 2 = 9,6 : 2 = 4,8 см
ΔAMO - прямоугольный, ∠AMO = 90°
По теореме Пифагора:
AM² = AO² - OM²
AM = 6,4 см
Прямоугольные треугольники AMO и AOB подобны по общему острому углу MAO.
AB = 10 см
Площадь ромба равна произведению стороны на высоту:
см²
Ответ: 96 см²
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад