Question

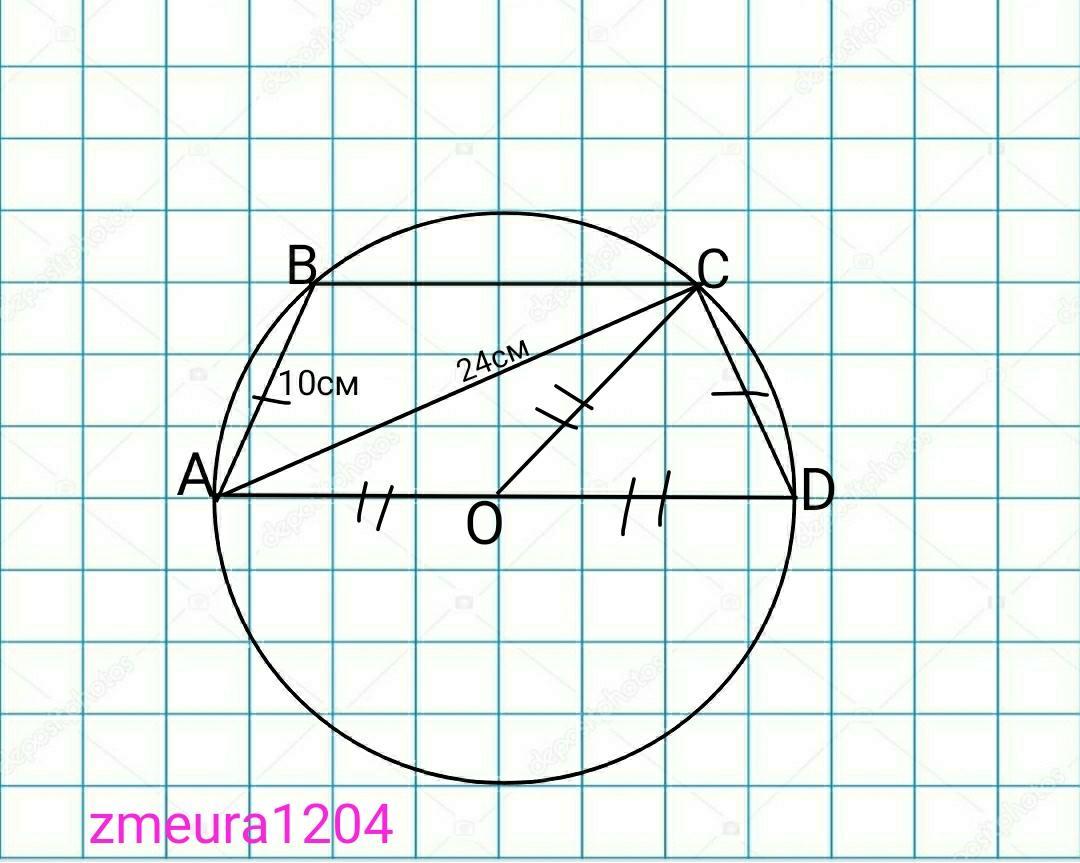
Трапеция ABCD вписана в ок-
ружность, центр О кото-
рой лежи
т на большем основании
AD. Найдите радиус описанной
окружности, если АВ=10 см,
AC=24 см.

​

Answer 1

Ответ:

R=13см

Объяснение:

Дано

О- центр окружности

ABCD- трапеция.

АВ=10см

АС=24см

R=?

Решение.

В окружность можно вписать равнобокую трапецию.

АВ=СD=10см.

∆АСD- прямоугольный треугольник.

<АСD=90°

По теореме Пифагора найдем

АD=√(AC²+CD²)=√(24²+10²)=√(576+100)=

=√676=26см.

R=OC

OC=AO=OD

R=AD:2=26:2=13cм

Zmeura1204