Ответы
Ответ дал:
8
Ответ:
Пошаговое объяснение:
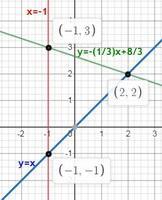
уравнение прямой проходящей через две точки
прямая AB
здесь , значит уравнение прямой в каноническом виде будет выглядеть непрезентабельно.
эта прямая параллельна оси OY, а ее уравнение можно записать в виде:
x = -1
прямая ВС
прямая СА
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад