Ответы
Ответ дал:
5
Ответ:
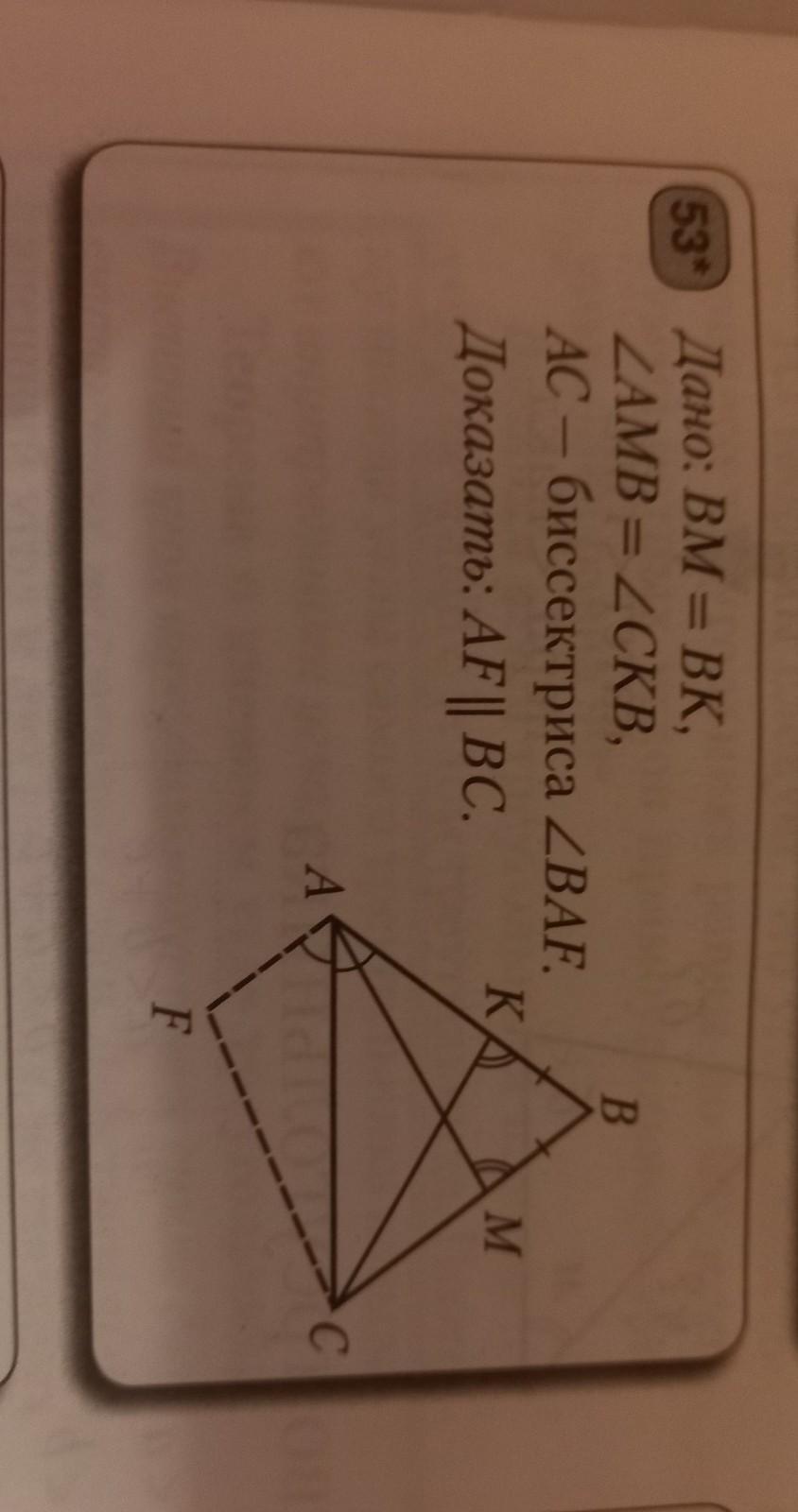
ΔАВС - равнобедренный по условию ⇒ ∠А = ∠С
Рассмотрим треугольники ВАК и ВСМ:
∠А = ∠С
АВ = ВС
АК = МС
Следовательно, ΔВАК = ΔВСМ по двум сторонам и углу между ними.
В равных треугольниках соответствующие стороны равны, отсюда:
ВМ = ВК, что и требовалось доказать.
Пошаговое объяснение:
lebedev20071610:
эм это не то
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад