α – острый угол параллелограмма ABCD. AB = 3 см, BC = 5 см, tgα = 2. Найди площадь параллелограмма ABC
Аноним:
я хочу баллыыыыыы
можно норм ответ
Ответы
Ответ дал:
3
Ответ:
см²
Объяснение:
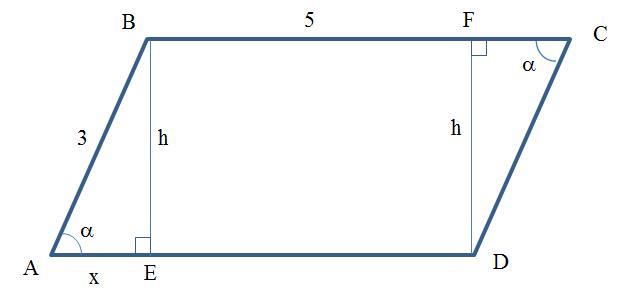
Дано (см. рисунок):
Параллелограмм ABCD
AB = 3 см
BC = 5 см
α = ∠BAE – острый угол параллелограмма
tgα = 2
Найти: площадь параллелограмма S.
Решение. Проведём высоту h = BE = DF параллелограмма и введём обозначение x = AE = CF. По определению
Отсюда
h = tgα·x = 2·x.
Так как треугольник ABE прямоугольный с гипотенузой AB, то можно применит теорему Пифагора:
AB² = AE² + BE² или 3² = x² + h² или 3² = x² + (2·x)².
Отсюда
5·x² = 9 или x = 3/√5.
Площадь параллелограмма определяется через сторону AD и высоту h по формуле:
S = AD·h.
Тогда
S = AD·h = 5·h = 5·2·x = 5·2·3/√5 = 6√5 см².
Приложения:
Вас заинтересует
2 года назад
2 года назад
9 лет назад