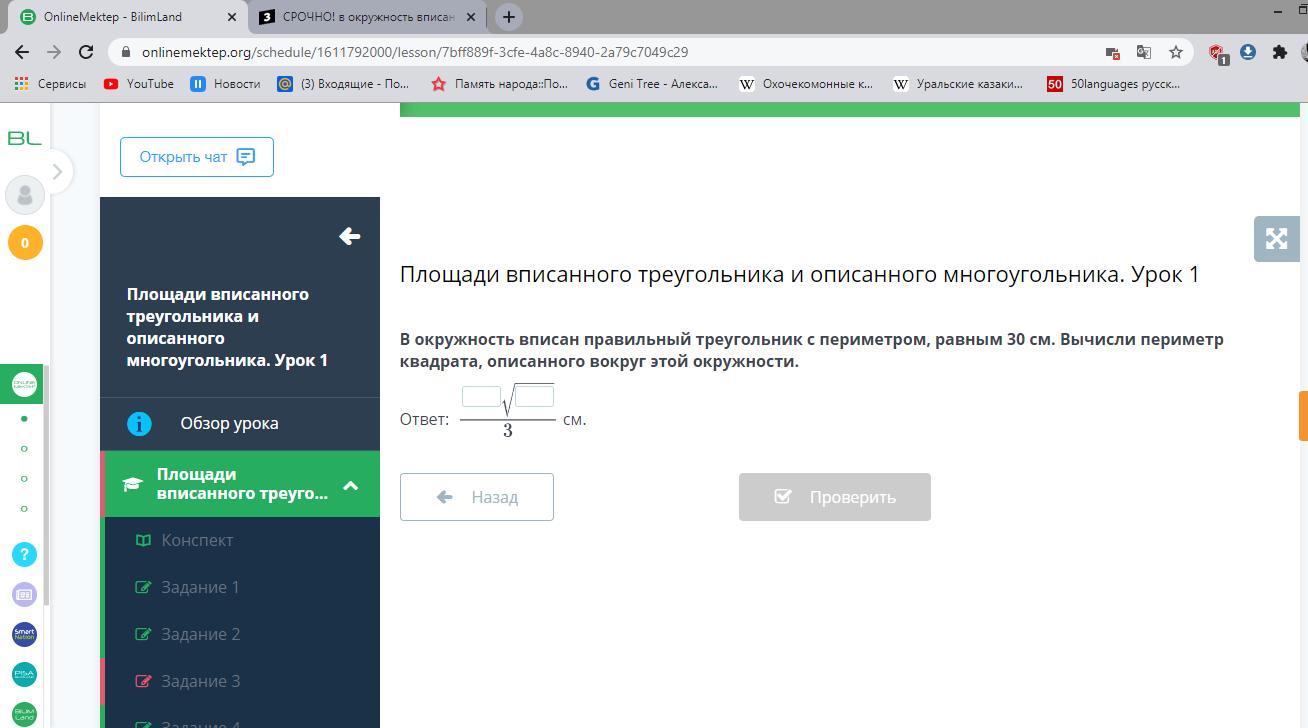
СРОЧНО ПОМОГИТЕ! В окружность вписан правильный треугольник с периметром, равным 30 см. Вычисли периметр квадрата, описанного вокруг этой окружности.
Приложения:
Ответы
Ответ дал:
7
Ответ:
(см)
Объяснение:
Радиус окружности, описанной около равностороннего треугольника равен:
Стороны треугольника равны. Зная периметр, можем найти сторону а:
(см) ⇒
(см)
Сторона квадрата с, описанного около окружности, равна ее диаметру:
(см)
Периметр квадрата равен:
(см)
Избавимся от иррациональности в знаменателе:
(см)
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад