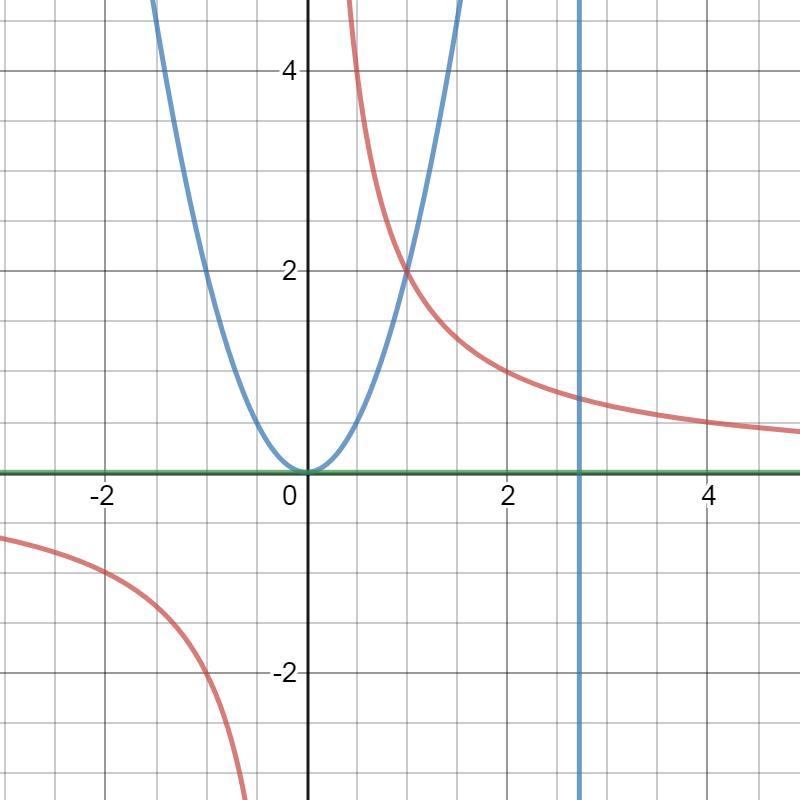
Вычислите площадь фигуры, ограниченной линиями y = 2x^2 , y = 2/x и x=e , y = 0
Аноним:
Такое делаю, как раз обеденный перерыв. Можете написать в вк, помогу. https://vk. com/id627897252
Ответы
Ответ дал:
3
Объяснение:
Ответ: S=2,66667 кв. ед.
Приложения:
Вас заинтересует
2 года назад
8 лет назад
9 лет назад