Question

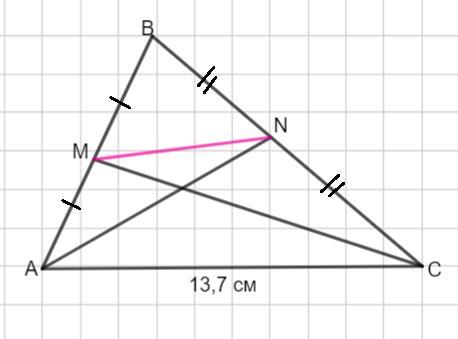
В треугольнике ABC сторона AC=13,7 см и проведены медианы CM и AN. Найди расстояние между M и N (запиши десятичную дробь).

Answer 1

Ответ:

6,85 см.

Объяснение:

Так как СМ - медиана, то точка М - середина стороны  АВ.

AN - медиана , то  N  - середина стороны BC.

Расстояние между точками M и  N - это длина отрезка  MN.

Отрезок  MN - это отрезок, соединяющий середины двух сторон треугольника. Значит, этот отрезок MN-  средняя линия треугольника АВС .

Средняя линия треугольника параллельна стороне треугольника и равна ее половине .

$MN= \dfrac{1}{2} \cdot AC;\\MN= \dfrac{1}{2} \cdot13,7 =13,7:2= 6,85$

$MN= 6,85$ см.