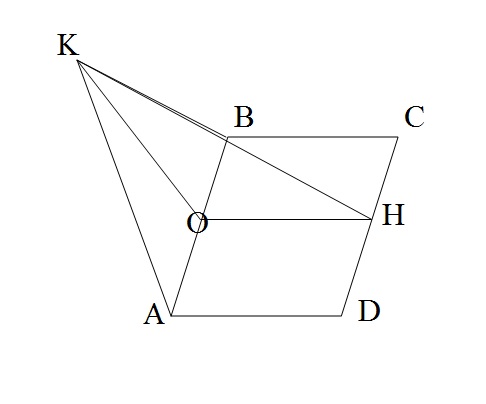
Плоскости прямоугольника ABCD и равнобедренного треугольника АВК перпендикулярны.АК = KB = 10 см, АВ = 16 см, AD = 8 см. Вычислите расстояние от точки К до середины стороны DC прямоугольника.
Ответы
Ответ дал:
0
Рассмотрим треугольник АКВ-равнобедренный (АК=КВ=10).
Проведем из т.К перпендикуляр КО.
Рассмотрим треугольник АОК-прямоугольный.
АО=1/2 АВ=8
ОК^2=AK^2-AO^2
OK=6.
Плоскости АВСD и АВК перпендикулярны, поэтому КО перпендикулярна ABCD.
Следовательно треугольник КОН-прямоугольный. Расстояние от точки К до прямой CD - прямая КН.
Рассмотрим треугольник КОН-прямоугольный.
КН^2=KO^2+OH^2
OH=AD=8
KH=10
Проведем из т.К перпендикуляр КО.
Рассмотрим треугольник АОК-прямоугольный.
АО=1/2 АВ=8
ОК^2=AK^2-AO^2
OK=6.
Плоскости АВСD и АВК перпендикулярны, поэтому КО перпендикулярна ABCD.
Следовательно треугольник КОН-прямоугольный. Расстояние от точки К до прямой CD - прямая КН.
Рассмотрим треугольник КОН-прямоугольный.
КН^2=KO^2+OH^2
OH=AD=8
KH=10
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
11 лет назад