Question

В основании пирамиды лежит прямоугольный треугольник с катетами 15 и 15√3. Каждое боковое ребро пирамиды наклонено к плоскости основания под углом arctg2√3 / 225. Найдите объем пирамиды.
Очень нужно.

Answer 1

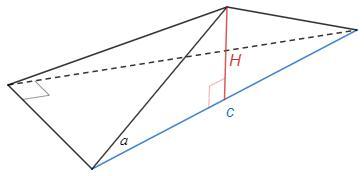
Опустим высоту H на основание.

Прямоугольные треугольники, образованные боковыми ребрами и высотой, равны по катету и острому углу.

Следовательно проекция вершины на основание равноудалена от вершин основания.

То есть вершина проецируется в центр описанной окружности основания.

Центр описанной окружности прямоугольного треугольника - середина гипотенузы c.

с= √(15^2 + 15^2*3) =15*2

H= c/2 *tga =15 *2√3/225 =2√3/15

√= 1/3 *S_осн *H =1/3 *1/2 *15*15√3 *2√3/15 =15