Question

Дан треугольник АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС этого треугольника в А1, а сторону ВС – в точке В1. Длина отрезка АС равна 6 см; А1В1 : АВ = 2 : 3. Найдите длину отрезка А1С.

Answer 1

Ответ:

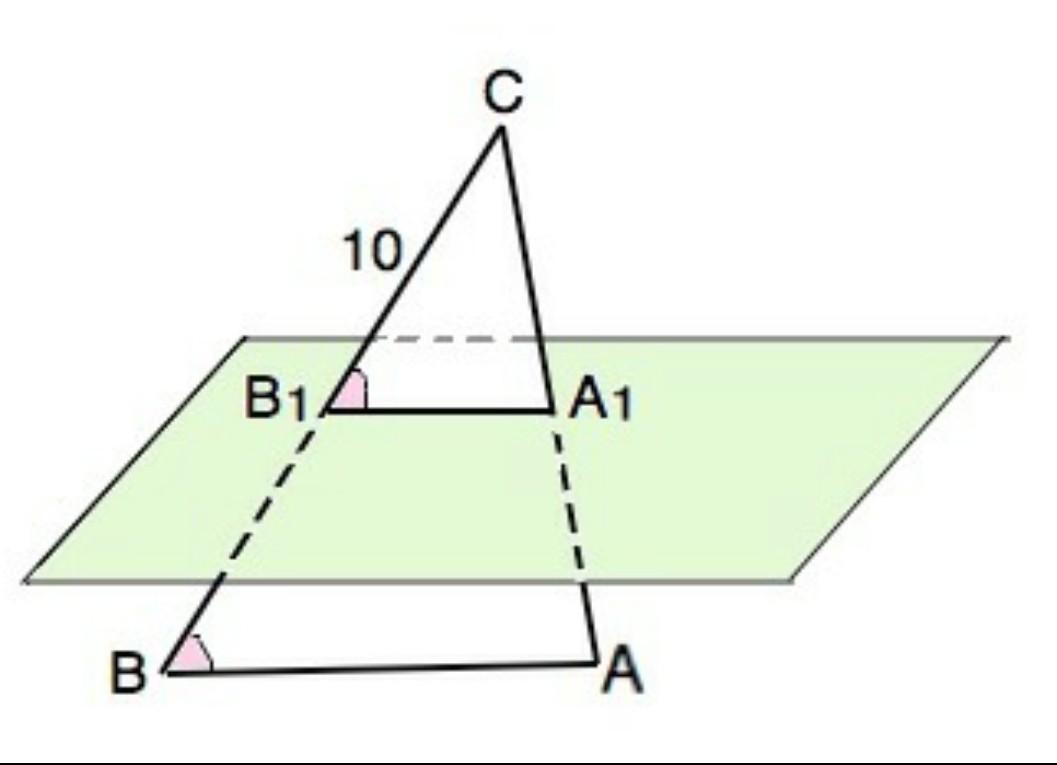
Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.Плоскость треугольника АВС проходит через прямую АВ, параллельную данной плоскости, и пересекает эту плоскость, следовательно, линия пересечения этих плоскостей В1А1 АВ. Поэтому в ДАВС и ДА1В1С ZСВ1А-ZСВА как соответственные при пересечении параллельных прямых АВ и А1B1 секущей ВС, ZC -общий эти треугольники подобны. Из подобия следует отношение: А1B1:10-4:5 БА1B1-40 — А1B1-8 см