Question

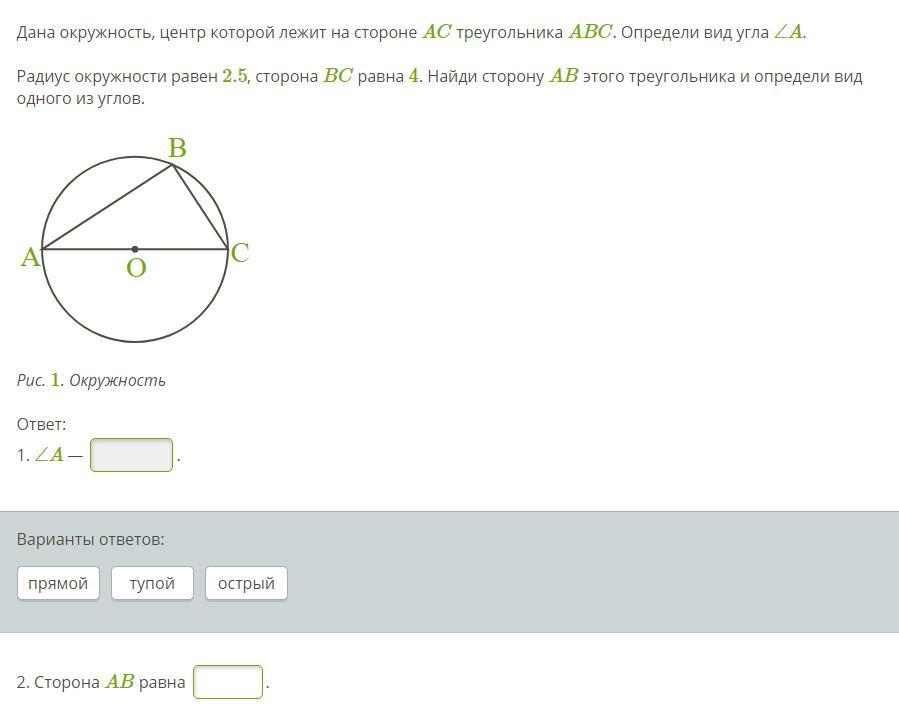
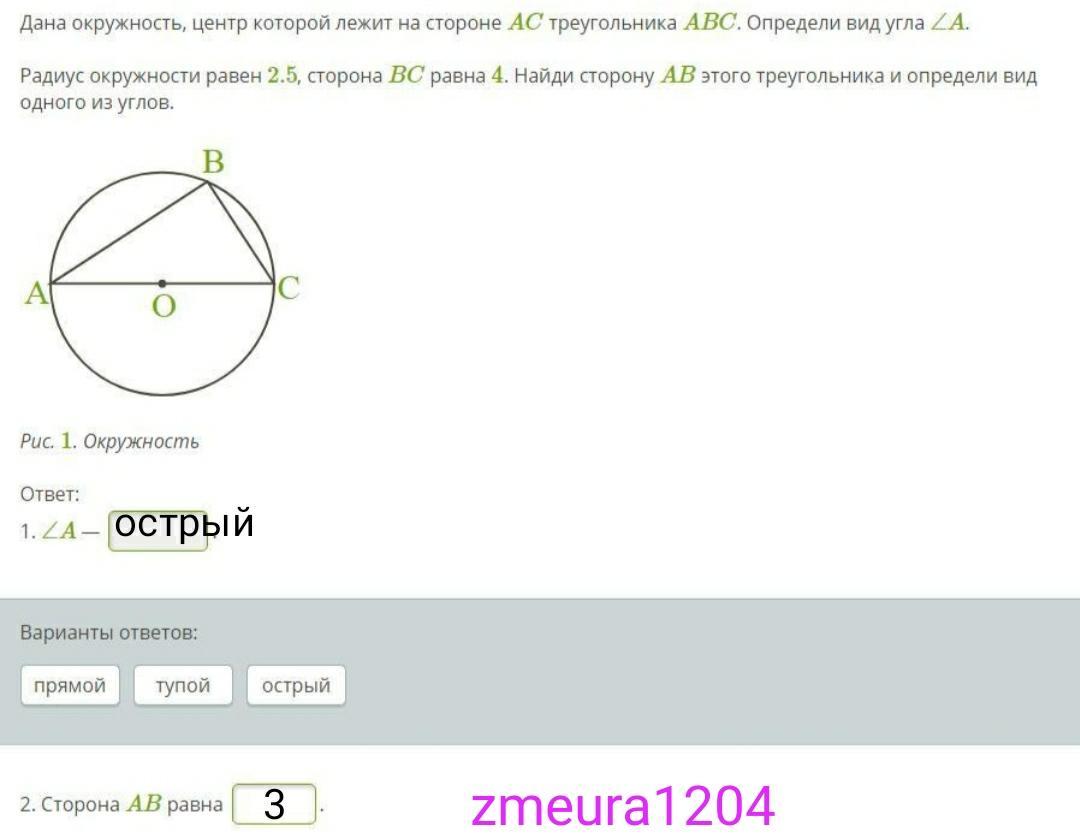
Дана окружность, центр которой лежит на стороне AC треугольника ABC. Определи вид угла ∠A.

Радиус окружности равен 2.5, сторона BC равна 4. Найди сторону AB этого треугольника и определи вид одного из углов.

Ответ:
1. ∠A —
2. Сторона AB равна

Answer 1

Ответ:

Объяснение:

<В - опирается на дугуАС 180° <В- вписанный угол равен половине дуги на которую опирается.

<В=дугаАС/2=180°:2=90°

<B=90°,

∆АВС- прямоугольный треугольник

В прямоугольном треугольнике один угол прямой (<В=90°), два оставшихся угла всегда острые.

<А- острый.

АО=2,5 радиус

АС- диаметр,

Диаметр окружности равен двум радиусам

АС=2*АО=2*2,5=5.

∆АВС- прямоугольный треугольник

АВ; ВС- катеты

АС- гипотенуза.

Теорема Пифагора

АВ=√(АС²-ВС²)=√(5²-4²)=√(25-16)=√9=3