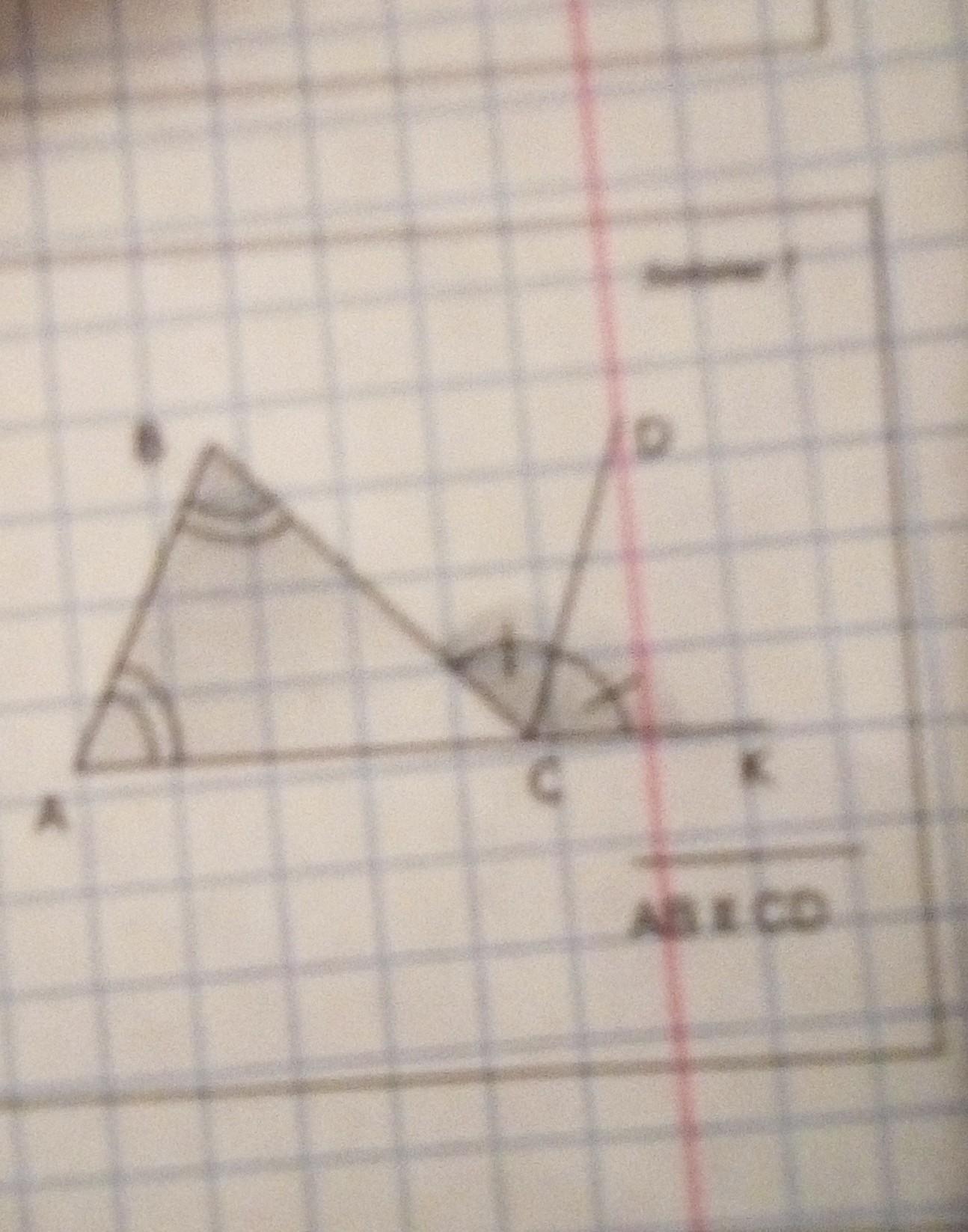Question

Угол А=углу В, СD-биссектриса. ДОКАЗАТЬ: AB||CD​

Answer 1

Объяснение: 1)∠BCK = ∠A+∠B (т.к. ∠BCK - внешний для ΔABC)

2) Т.к. CD - биссектриса, то ∠BCK = 2∠BCD=2∠DCK

3)∠А=∠B (по условию)

Из 1,2,3  следует, что

∠BCK = ∠A+∠B

∠BCK = 2∠BCD

∠А=∠B

Значит, ∠B=∠BCD, а они, в свою очередь, накрест лежащие углы для АВ и CD, следовательно, AB||CD​