Question

Линейное неравенство с одной переменной. Решение линейных неравенств с одной переменной. Урок 2

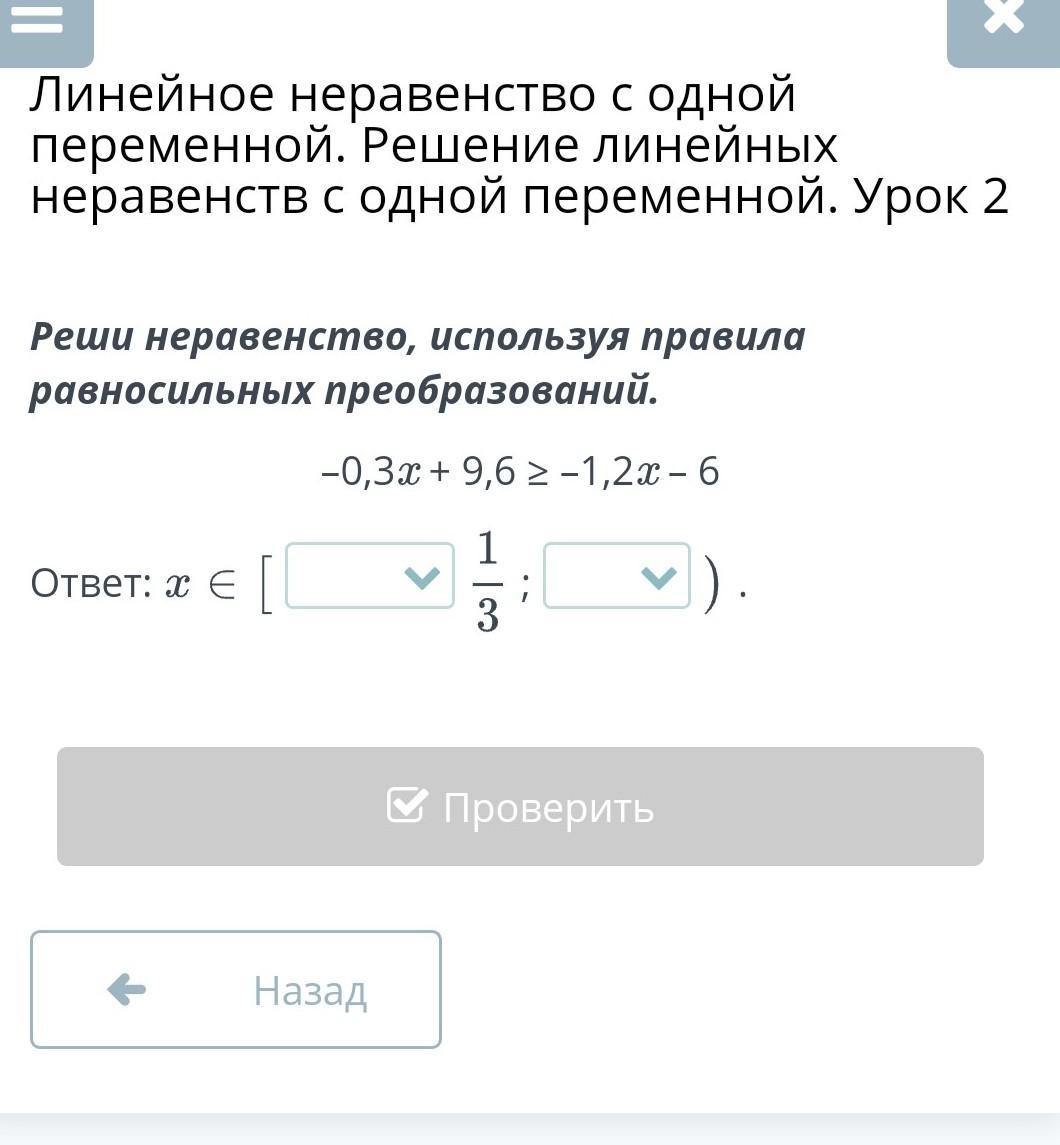
Реши неравенство, используя правила равносильных преобразований.



​

Answer 1

Ответ:

$\displaystyle x \in \bigg [-17\frac{1}{3} ;+\infty\bigg )$

Пошаговое объяснение:

Определения:

• ◊ равносильные преобразования неравенств это некоторые действия с правой и левой частью неравенств, в результате которых мы получаем новые неравенства, равносильные исходным.

• ◊ равносильные неравенства - это неравенства, имеющие одни и те же решения.

Правила преобразования неравенств:

правило 1:

• Любой член неравенства можно переносить из одной части неравенства в другую, меняя при этом знак на противоположный (т.е. при переносе через знак неравенства знаки при слагаемых меняются на противоположные).

правило 2:

• Обе части неравенства можно умножить/разделить на одно и то же положительное число, при этом получится неравенство, равносильное данному.

правило 3:

• Обе части неравенства можно умножить/разделить на одно и то же отрицательное число, меняя знак неравенства на противоположный (т.е. знак > на знак <, и наоборот; знак ≥на знак ≤, и наоборот).

Приступим.

Наше неравенство

-0.3х +9.6 ≥ -1.2х -6

Воспользуемся правилом 1, перенесем все члены с х влево, свободные члены - вправо.

-0.3х +1.2х  ≥ -9.6 -6

Приведем подобные

0.9х  ≥ -15.6

Воспользуемся правилом 2 и разделим обе части неравенства на 0.9. Найдем решение неравенства

$\displaystyle x\geq (-15.6):0.9\\\\x\geq \bigg (-15\frac{6}{10}\bigg ) :\frac{9}{10} \\\\\\x\geq \bigg (-\frac{156}{10} \bigg)*\frac{10}{9} \\\\\\\displaystyle x\geq -\frac{156}{9} \\\\x\geq -17\frac{1}3} \\\\\boldsymbol {x \in \bigg [-17\frac{1}{3} ;+\infty\bigg )}$