Question

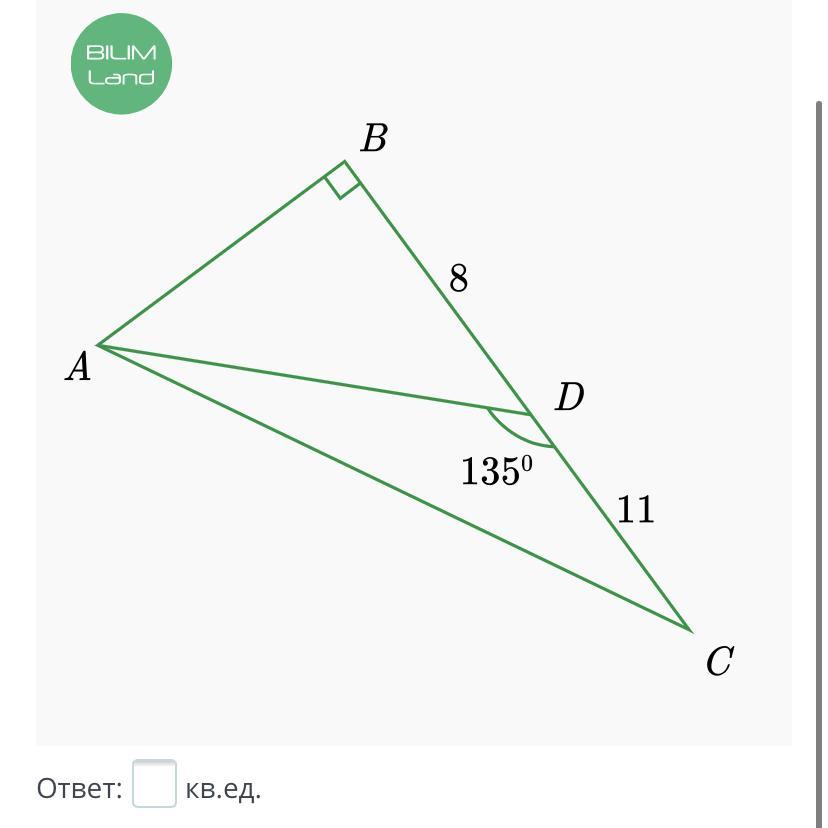
ABC – прямоугольный треугольник,
BD = 8, DC = 11, ∠ADC = 135°.
Найди площадь треугольника ADC

Answer 1

Ответ:

S(ADC)=44 ед²

Объяснение:

<BDC=180° развернутый угол.

<BDA=<BDC-<ADC=180°-135°=45°

Сумма углов в треугольнике равна 180°

<ВАD=180°-<ABD+<BDA=180°-90°-45°=45°

∆BAD- равнобедренный треугольник

(90°;45°;45° углы при основании равны) АВ=BD=8

Площадь прямоугольного треугольника равна половине произведения двух катетов

S(ABC)=1/2*AB*BC=1/2*8*19=76 ед²

S(ABD)=1/2*AB*BD=1/2*8*8=32 ед²

S(ADC)=S(ABC)-S(ABD)=76-32=44 ед²