Question

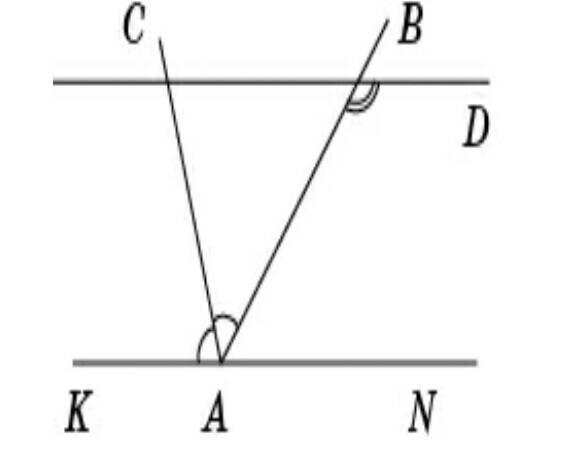
Через параллельные прямые CD и AK проведена секущая BA так, что угол ∠DBA = 130°.
АС — биссектриса угла BAK. Найдите ∠CAB.
Решение.
Так как прямые CD// AK по условию, то ∠ ?= ∠KAB . Значит,
∠DBA = ∠ =_0 .
АС — биссектриса∠ ВАК по условию => ∠KAC = ∠ ?. Поэтому ∠CAB =∠ _ =_0 .
Ответ: ∠CAB =__0 .
дам 34 балла​

Answer 1

Ответ:

Объяснение:

Смотри.

1.BAK=DBA=130 (накрест леж углы)

2.АС - биссек

3.из 1 и 2п => BAC=1/2BAK=65

Answer 2

Ответ:

угол САВ=25 градусов...