Определите скорость колеблющегося тела в момент времени t ,если координата,изменяется по закону о(t) (x- в метрах,t- в секундах)
Приложения:
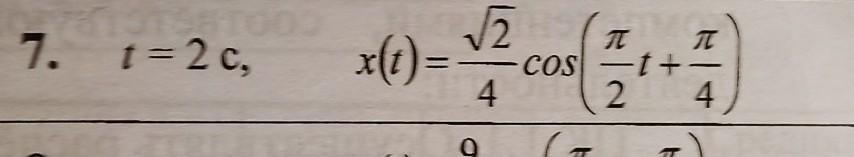
Ответы
Ответ дал:
0
Ответ:
Скорость можно найти по формуле:
подставляем
t = 2c
Ответ: П/8 м/с (примерно 0,4 м/с)
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад