Question

Срочно нужна помощь!! 30 баллов!​

Answer 1

Рассмотрим ΔBOC:

По условию:

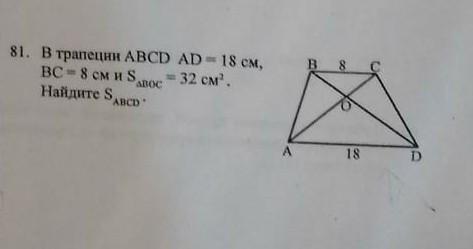
BC = 8 см;

S(ΔBOC) = ½BC•h1 = 32 см²,

где: h1 - высота ΔBOC при основании BC.

Следовательно:

h1 = 2S(ΔBCO)/BC = 2•32/8 = 8 см.

Рассмотрим ΔBOC и ΔAOD:

<AOD = <BOC (как вертикальные);

<OAD = <OCB; <ODA = <OBC (как накрест лежащие).

Значит ΔBOC ~ ΔAOD (подобные):

Пусть h2 - высота ΔAOD при основании AD.

Тогда:

h2/h1 = AD/BC => h2 = h1•AD/BC

h2 = 8•18/8 = 18 см.

Как видим высота трапеции ABCD равна:

H = h1 + h2 = 8 + 18 = 26 см.

Тогда:

S(ABCD) = ½(BC + AD)•H =

= ½(8 + 18)•26 = 13•26 = 338 см².