Question

  Решите задачу по геометрии (желательно с рисунком).
Диагонали трапеции ABCD с основаниями AB и CD пересекаются в точке O. Найти а) AB если OB=4 OD=10 DC=25;  б) AO:OC и BO:OD,если AB=A, DC=B. в) AO, если AB=9,6 дм, DC=24 см, AC-15 см.

Answer 1

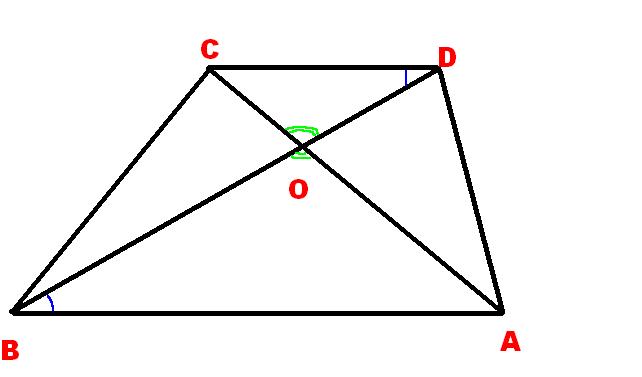
Треугольники АВО и CDO подобны по двум углам. Значит:

$frac{AB}{CD} = frac{OB}{OD} \ frac{AB}{25} = frac{4}{10} \ AB=10$

$frac{AO}{OC} = frac{AB}{CD} = frac{a}{b} \ frac{BO}{OD} = frac{AB}{CD} = frac{a}{b}$

$frac{AB}{DC} = frac{AO}{OC} = frac{AC-OC}{OC} = frac{AC}{OC}-1 \ frac{96}{24} = frac{15}{OC}-1 \ OC= 3 \ AO=AC-AO=15-3=12$