Question

Дано тетраедр ABCD . М принадлежит DВ, N принадлежит DВ. DN=MN=NB.Постройте сечение тетраедра, плоскостью которая проходит через точку М параллельно плоскости АNС. Вычислите периметр и площадь сечения, если AN=CN=25см,  AC=14см.

Answer 1

Решение во вложениях.

Answer 2

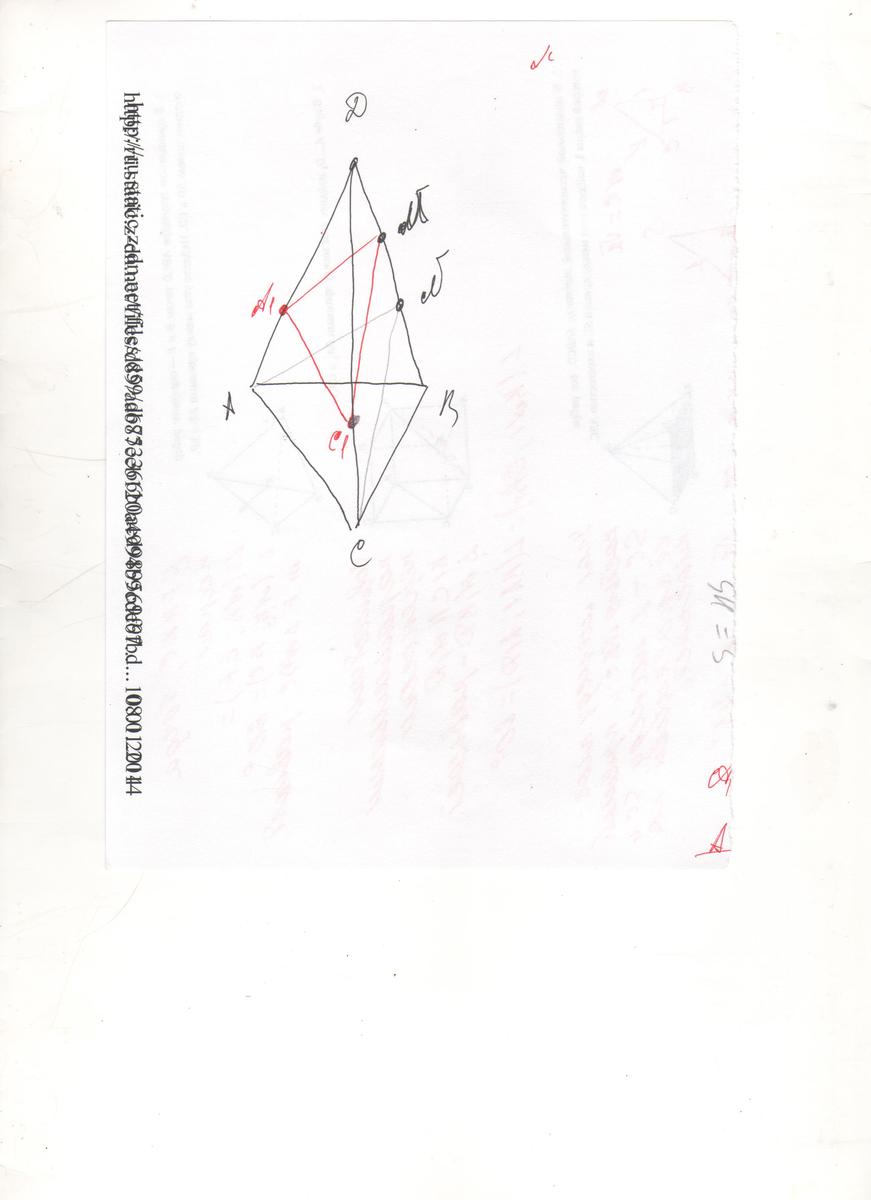
Сечение плоскости параллельное плоскости параллельно ACN
1. Провести прямую С1M || CN
2. Провести прямую A1M || AN
3. Прямая А1C1 ||   АС

Периметр ΔА1С1N

1. ΔADC, ΔA1DC1 - подобны с коэффициентом подобия 2/3
А1С1=АС:3*2=14*2:3= 28/3

2. ΔCND, ΔC1ND - подобны с коэффициентом подобия 1/2
С1M=A1M=СN:2=25/2
P=A1C1+A1N+C1N=28/3+25=34 1/3 периметр искомого сечения
 
В равнобедренном ΔA1C1M, высота проведенная к основанию А1С1 - разбивает его на два равных прямоугольных треугольника с  гипотенузой 25/2 и катетом 14/3, по т. Пифагора находим катет
          25²       14²           5625 - 784                       4841
h²=   -----  -   ------  =--------------------------- =   ---------------
           4          9                 36                                36
S=(28:3*√4841:6):2  =28√481:9
что-то далеко НЕ классическое, но.........