Ответы
Ответ:
1)105° 2)110°
Объяснение:
#1
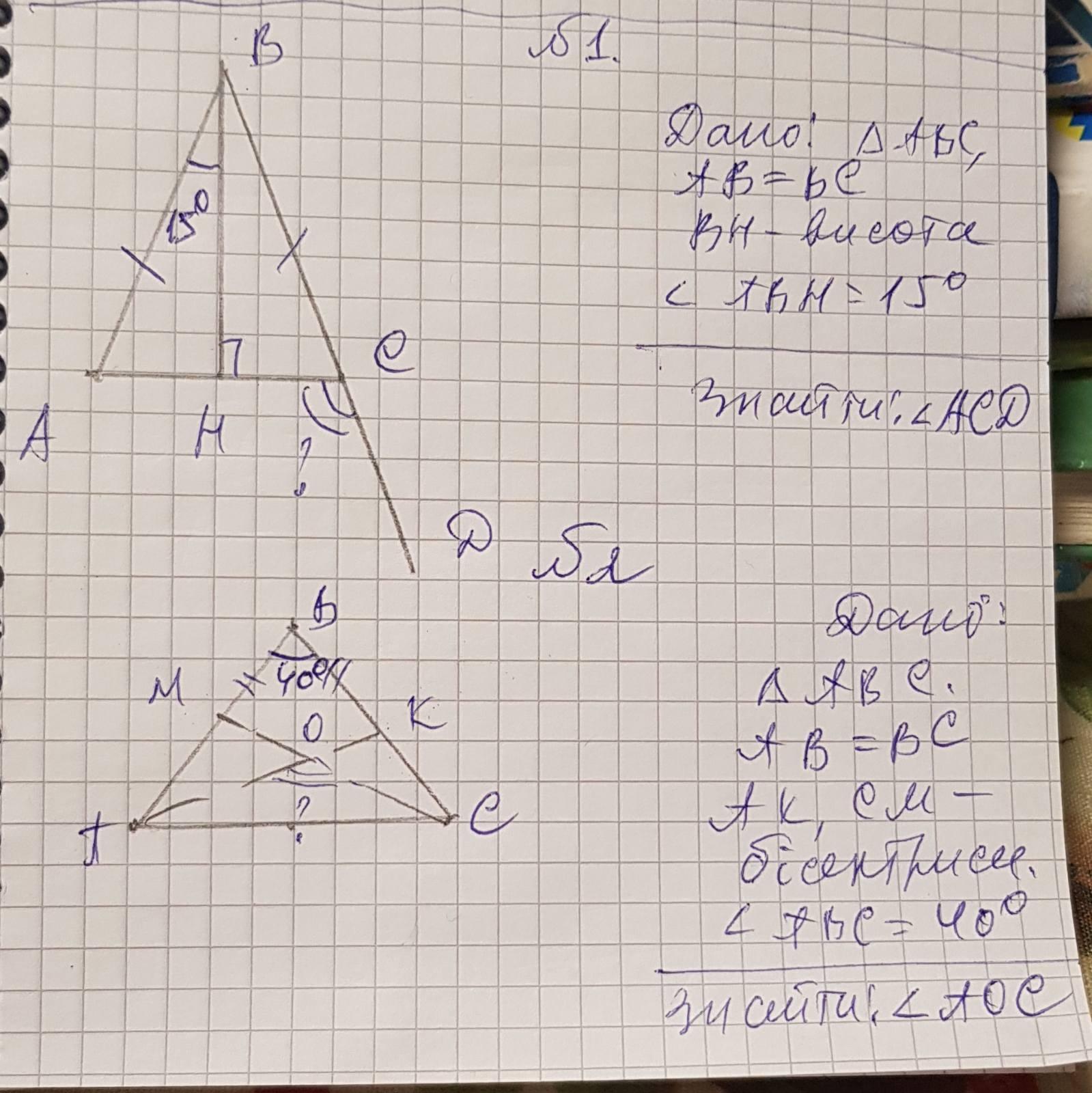
1) Так как треугольник АВС - равнобедренный, высота, проведённая к основанию, является также биссектрисой и медианой. Поэтому, ∠АВН = ∠НВС = 15°
2) Учитывая что сумма углов в треугольнике равна 180°, ∠ВСА = 180° - ∠НВС - ∠ВНС = 180° - 15° - 90° = 75°
3) ∠АСD - внешний угол △ АВС
∠АСD = 180° - ∠ВСА = 180° - 75° = 105°
#2
1) Так как АК и СМ - биссектрисы, то пускай ∠ВАК = ∠КАС = α, а ∠ВСМ = ∠МСА = β. Тогда, угол, который нам нужно найти равен:
180° - α - β = 180° - (α + β) (т.к. сумма углов в треугольнике равна 180° , а мы рассматриваем △АОС)
2) Рассмотрим △АВК.
∠ВКА = 180° - ∠АВК - ∠ВАК = 180° - 40° - α = 140° - α
3) Рассмотрим △АКС.
∠АКС = 180° - ∠КАС - ∠АСК = 180° - α - 2β
4) Сумма смежных углов равна 180°, а значит:
∠BKA + ∠AKC = 180°
140° - α + 180° - α - 2β = 180°
140° - 2α - 2β = 0
2α + 2β = 140°
α + β = 70°
А угол, который нам надо найти, напомню, равен 180° - (α + β)
Поэтому:
5) ∠AOC = 180° - (α + β) = 180° - 70° = 110°