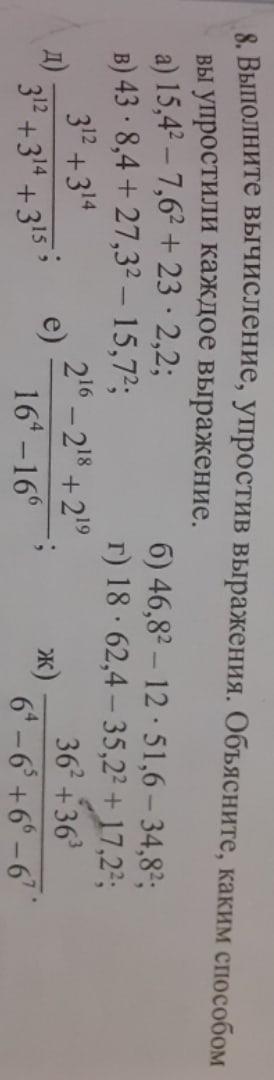Ответы
Ответ:
Пошаговое объяснение:
а) 15,4²-7,6²+23·2,2=(15,4-7,6)(15,4+7,6)+23·2,2=7,8·23+23·2,2=23(7,8+2,2)=23·10=230 - (формула разности квадратов; вынесение общего множителя за скобки)
б) 46,8²-12·51,6-34,8²=(46,8-34,8)(46,8+34,8)-12·51,6=12·81,6-12·51,6=12(81,6-51,6)=12·30=360 - (формула разности квадратов; вынесение общего множителя за скобки)
в) 43·8,4+27,3²-15,7²=43·8,4+(27,3-15,7)(27,3+15,7)=43·8,4+11,6·43=43(8,4+11,6)=43·20=860 - (формула разности квадратов; вынесение общего множителя за скобки)
г) 18·62,4-35,2²+17,2²=18·62,4-(35,2-17,2)(35,2+17,2)=18·62,4-18·52,4=18(62,4-52,4)=18·10=180 - (формула разности квадратов; вынесение общего множителя за скобки)
д) (3¹²+3¹⁴)/(3¹²+3¹⁴+3¹⁵)=(3¹²(1+3²))/(3¹²(1+3²+3³))=10/37 - (вынесение общего множителя за скобки)
е) (2¹⁶-2¹⁸+2¹⁹)/(16⁴-16⁶)=(2¹⁶(1-2²+2³))/(16⁴(1-16²))=5/(-255)=-1/51 - (вынесение общего множителя за скобки; приведение к общему основанию степени; сокращение дроби)
ж) (36²+36³)/(6⁴-6⁵+6⁶-6⁷)=(36²(1+36))/(6⁴(1-6+6²-6³))=(6⁴·37)/(6⁴(-5+36-216))=37/185=1/5=0,2 - (вынесение общего множителя за скобки; приведение к общему основанию степени; сокращение дроби)