Упростите выражение :
а) cos² δ ₋ ctg² δ
_____________ ;
sin² δ₋ tg² δ
б) tg³ β ₊ ctg³ β
______________ .
( tg β ₋ ctg β)²₊1
Ответы
Ответ дал:
0
1)(cos²b*sin²b-cos²b)/sin²b :(sin²b*cos²b-sin²b)/cos²b= cos²b(sin²b-1)/sin²b : sin²b(cos²b-1)/cos²b=cos²b*(-cos²b)/sin²b : sin²b*(-sin²b)*cos²b= -cos^4b/sin²b : -sin^4b/cos²b=cos^4b/sin²b*cos²b/sin^4b=cos^6b/sin^6b=ctg^6b
2)(tgb+ctgb)(tg²b-tgb*ctgb+ctg²b)/(tg²b-2tgb*ctgb+ctg²b-1)=
(tgb+ctgb)(tg²b-1+ctg²b)/(tg²b-2+ctg²b+1)=(tgb+ctgb)(tg²b-1+ctg²b)/(tg²b+ctg²b-1)=
(tgb+ctgb)=(sinb*sinb+cosb*cosb)/sinb*cosb=(sin²b+cos²b)/1/2sin2b=2/sin2b
2)(tgb+ctgb)(tg²b-tgb*ctgb+ctg²b)/(tg²b-2tgb*ctgb+ctg²b-1)=
(tgb+ctgb)(tg²b-1+ctg²b)/(tg²b-2+ctg²b+1)=(tgb+ctgb)(tg²b-1+ctg²b)/(tg²b+ctg²b-1)=
(tgb+ctgb)=(sinb*sinb+cosb*cosb)/sinb*cosb=(sin²b+cos²b)/1/2sin2b=2/sin2b
Ответ дал:
0
решение смотри во вложении
Приложения:
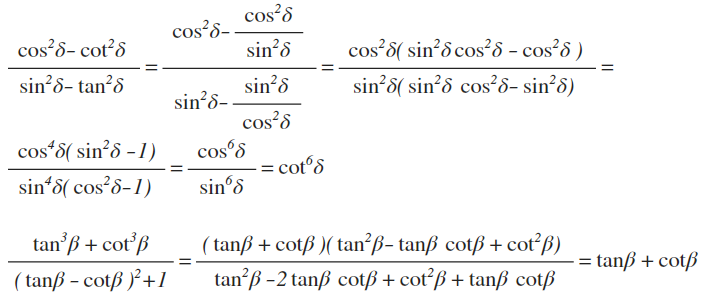
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
11 лет назад