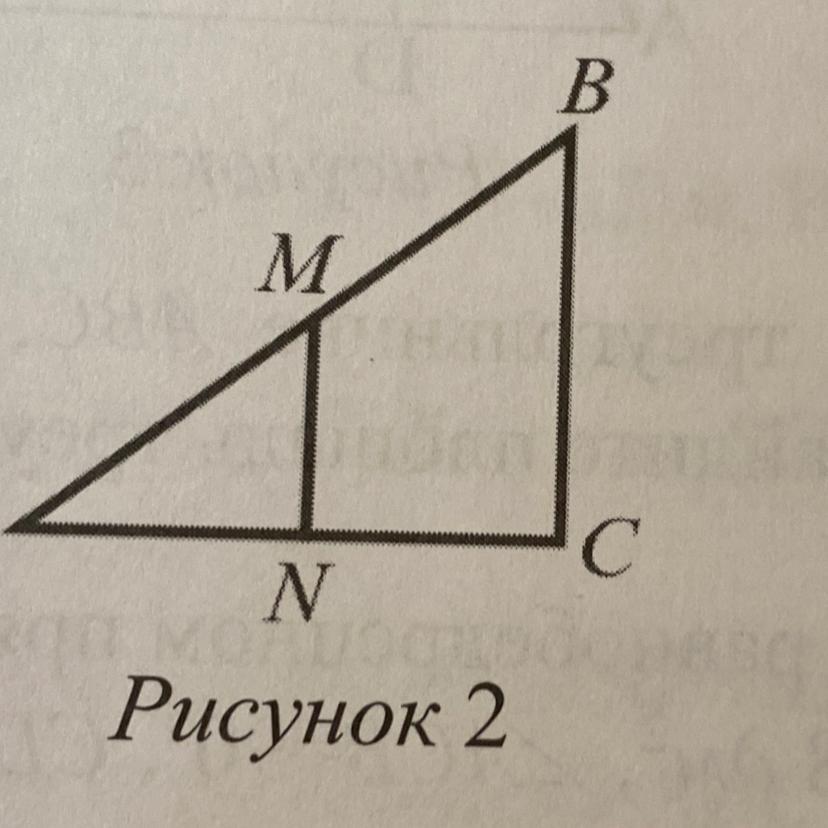
В треугольнике ABC, угол С=90 градусов, АМ=МB, MN перпендикулярно AC, МN=6 см, AC=16 см. Найдите площадь четырёхугольника MBCN (рисунок 2).
Приложения:
Ответы
Ответ дал:
3
Ответ:
96 см²
Пошаговое объяснение:
По теореме Фалеса, если АМ=МB, то и АN=NС.
Значит МN - средняя линия ΔАВС. Средняя линия треугольника равна половине основания, которому она параллельна, значит ВС=6*2=12 см.
Площадь прямоугольного треугольника равна половине произведения катетов, S=1/2 * 16 * 12 = 96 cм²
asura11:
вопрос-то о площади 4-х-угольника МNCB:) Наверное, её можно найти, отняв от площади всего треугольника=96 площадь маленького треугольника AMN, а она равна 1/2*8*6=24. то есть искомая площадь будет равна 96-24=72 кв.см.
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад