Ответы
Ответ дал:
3
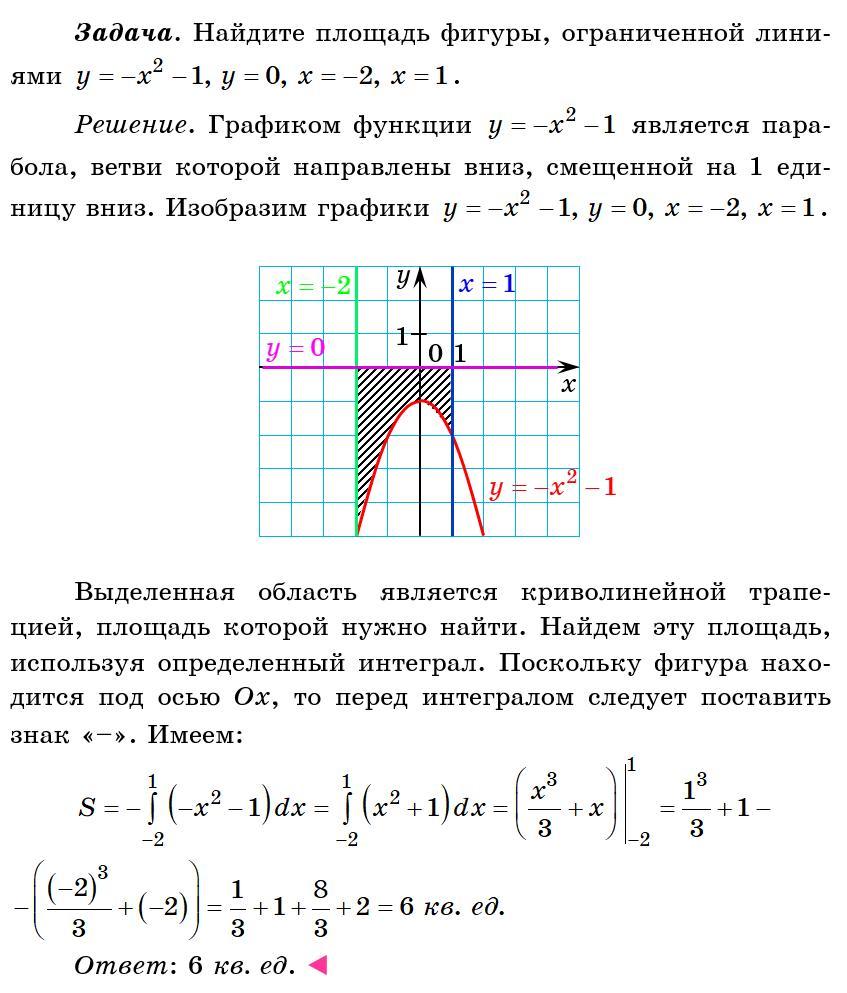
Найдите площадь фигуры, ограниченной линиями
Примечание. Площадь криволинейной трапеции (фигура, ограниченная графиком непрерывной на промежутке
функции
, осью
и прямыми
и
) вычисляется по формуле
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
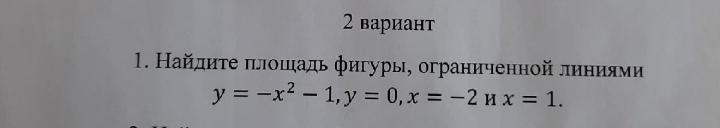
Примечание. Площадь SSкриволинейной трапеции (фигура, ограниченная графиком непрерывной на промежутке [a; ~ b][a; b] функции f(x)f(x) , осью OxOx и прямыми x=ax=a и x=bx=b ) вычисляется по формуле
\boxed{S = \displaystyle \int\limits_a^b f(x)\,dx}S=a∫bf(x)dx