Ответы
Ответ дал:
2
Ответ:
Смотри решение на фото
Приложения:
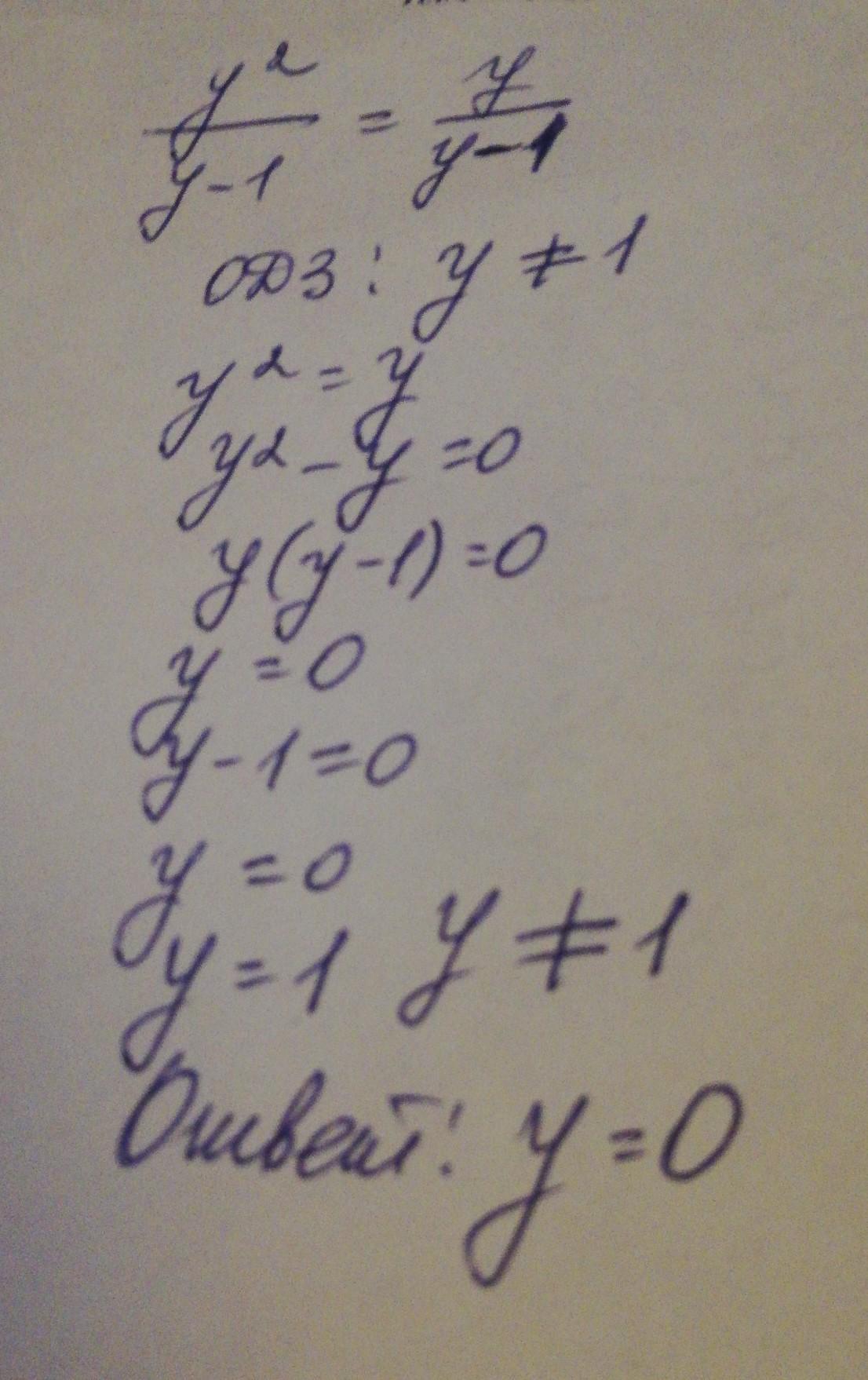
Ответ дал:
4
Решить дробно рациональное уравнение  .
.
Перенесём дробь из правой части в левую, изменив её знак на противоположный (в правой части останется 0).
Так как знаменатели у дробей одинаковы, запишем числители обоих дробей над общим знаменателем.
Теперь запишем условие, при котором данное дробно рациональное уравнение будет иметь смысл.
ОДЗ:
------------------------------------------------------------------------------------------------
Произведение равно нулю только тогда, когда хотя бы один из множителей равен нулю.
или
- посторонний корень, т.к. y ≠ 1.
Ответ: y = 0.
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад