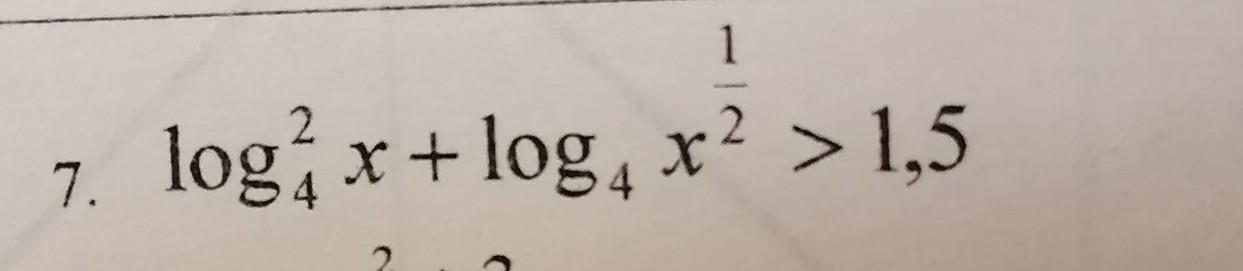Ответы
Ответ дал:
1
Для начала найдем область допустимых значений: х>0. Теперь можем решать:
1/2 можно вынести за логарифм по свойствам логарифмов.
Далее логарифм обозначим за t для удобства:
t^2+0,5t>1,5
Домножим обе части неравенства на два, чтобы избавиться от дробных чисел и перенесем 3 в левую часть:
2t^2+t-3>0
По теореме виета раскладываем на линейные множители:
(2t+3)(t-1)>0
Методом интервалов определяем, что условиям неравенства удовлетворяют
t<-1,5 и t>1
Возвращаем логарифмы:
log4(x)<-1,5 и log4(x)>1
Теперь любым удобным равносильным переходом добираемся до икса (числа в правых частях представить как log4(4^n), где n — наши числа, после логарифмы отбрасываются):
х<0,125 и х>4
Так как у нас есть ограничение х>0, окончательный ответ следующий:
0<х<0,125 и х>4
1/2 можно вынести за логарифм по свойствам логарифмов.
Далее логарифм обозначим за t для удобства:
t^2+0,5t>1,5
Домножим обе части неравенства на два, чтобы избавиться от дробных чисел и перенесем 3 в левую часть:
2t^2+t-3>0
По теореме виета раскладываем на линейные множители:
(2t+3)(t-1)>0
Методом интервалов определяем, что условиям неравенства удовлетворяют
t<-1,5 и t>1
Возвращаем логарифмы:
log4(x)<-1,5 и log4(x)>1
Теперь любым удобным равносильным переходом добираемся до икса (числа в правых частях представить как log4(4^n), где n — наши числа, после логарифмы отбрасываются):
х<0,125 и х>4
Так как у нас есть ограничение х>0, окончательный ответ следующий:
0<х<0,125 и х>4
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад