Question

а) Выбери решения уравнения 14sin2x+sin2x−4cos2x=4:

arctg810,+πn,n∈Z
−arctg810,+2πn,n∈Z
−arctg108,+πn,n∈Z
−arctg108,+2πn,n∈Z
−arctg810,+πn,n∈Z
−π4+πk,k∈Z
другой ответ
π4+πk,k∈Z
−3π4+πk,k∈Z
б) Посчитай количество корней, принадлежащих отрезку [2π;11π2].
Ответ:

Answer 1

Ответ:

$14 \sin {}^{2} (x) + 2 \sin(x) \cos(x) - 4 \cos {}^{2} (x) = 4 \\ 14 \sin {}^{2} (x) + 2 \sin(x) \cos(x) - 4 \cos {}^{2} (x) = 4 \sin {}^{2}(x ) + 4\cos {}^{2} (x) \\ 10 \sin {}^{2}(x ) + 2 \sin(x) \cos(x) - 8 \cos {}^{2} (x) = 0 \\ | \div \cos {}^{2} (x) \\ 10 {tg}^{2} x + 2tgx - 8 = 0 \\ 5 {tg}^{2} x + tgx - 4 = 0 \\ \\ tgx = t \\ \\ 5 {t}^{2} + t - 4 = 0 \\ d = 1 + 80 = 81 \\ t1 = \frac{ - 1 + 9}{10} = \frac{8}{10} = \frac{4}{5} \\ t2 = - 1 \\ \\ tgx1 = \frac{4}{5} \\ x1 = arctg \frac{4}{5} + \pi \: n \\ \\ tgx2 = - 1 \\ x2 = - \frac{\pi}{4} + \pi \: n$

n принадлежит Z.

Ответ: подходят варианты первый и шестой

б)

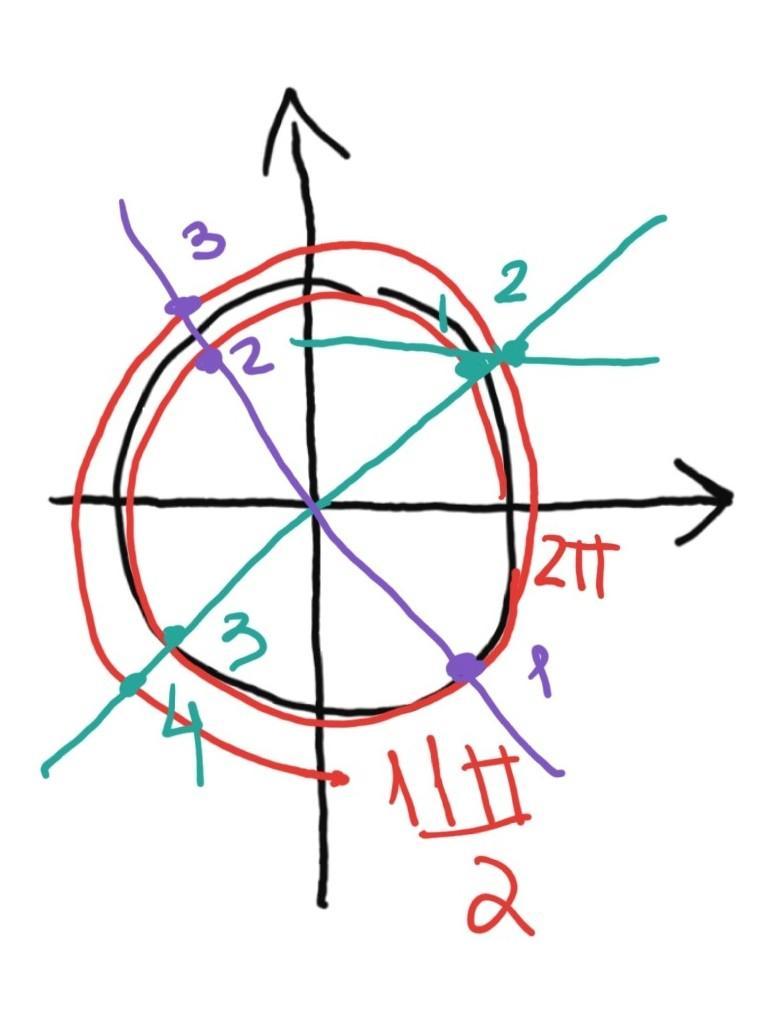
Посчитаем корни

рисунок

Ответ: 7