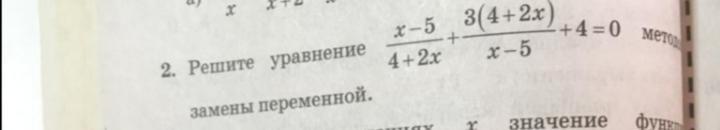Ответы
Ответ дал:
0
Ответ:
Объяснение:
ОДЗ: х ≠ 5; х ≠ -2
Замена переменной
Возвращаемся к замене
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад