Угол между диагоналями параллелограмма ABCD равен 60 градусов, AC=20см, BD=14. Найти периметр параллелограмма
Ответы
Ответ дал:
0
Диагонали параллелограмма точкой пересечения делятся пополам.
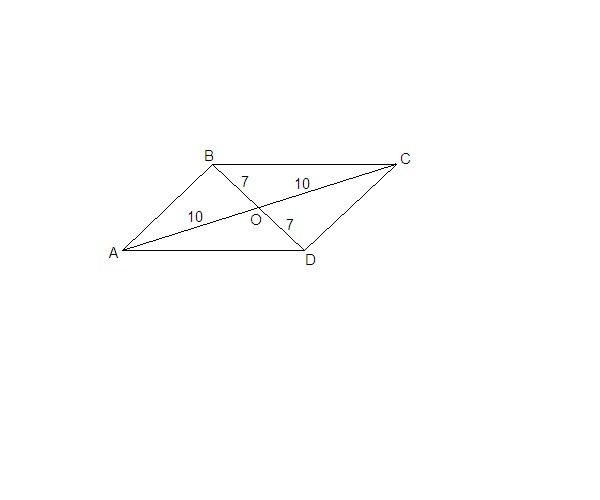
АО = ОС = 20/2 = 10 см
BO = OD = 14/2 = 7 см
ΔАОВ: по теореме косинусов
АВ² = AO² + BO² - 2AO·BO·cos60°
AB² = 100 + 49 - 2·10·7·1/2 = 149 - 70 = 79
AB = √79 см
СD = AB = √79 см
∠ВОС = 180° - ∠АОВ = 180° - 60° = 120° как смежные углы
ΔВОС: по теореме косинусов
BC² = OB² + OC² - 2·OB·OC·cos120°
BC² = 49 + 100 - 2·7·10·(- 1/2) = 149 + 70 = 219
BC = √219 см
CD = BC = √219 см
Pabcd = 2·(√79 + √219)
АО = ОС = 20/2 = 10 см
BO = OD = 14/2 = 7 см
ΔАОВ: по теореме косинусов
АВ² = AO² + BO² - 2AO·BO·cos60°
AB² = 100 + 49 - 2·10·7·1/2 = 149 - 70 = 79
AB = √79 см
СD = AB = √79 см
∠ВОС = 180° - ∠АОВ = 180° - 60° = 120° как смежные углы
ΔВОС: по теореме косинусов
BC² = OB² + OC² - 2·OB·OC·cos120°
BC² = 49 + 100 - 2·7·10·(- 1/2) = 149 + 70 = 219
BC = √219 см
CD = BC = √219 см
Pabcd = 2·(√79 + √219)
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад