Ответы
Ответ дал:
1
Ответ:
Объяснение:
ОДЗ:
Решение:
Решим уравнение по теореме Виета:
Корень х₂ не удовлетворяет ОДЗ.
juliaonesko:
спасибо большое, а вы можете её через дискриминант решить?
Ответ дал:
1
Ответ:
решение на фотографии
Приложения:

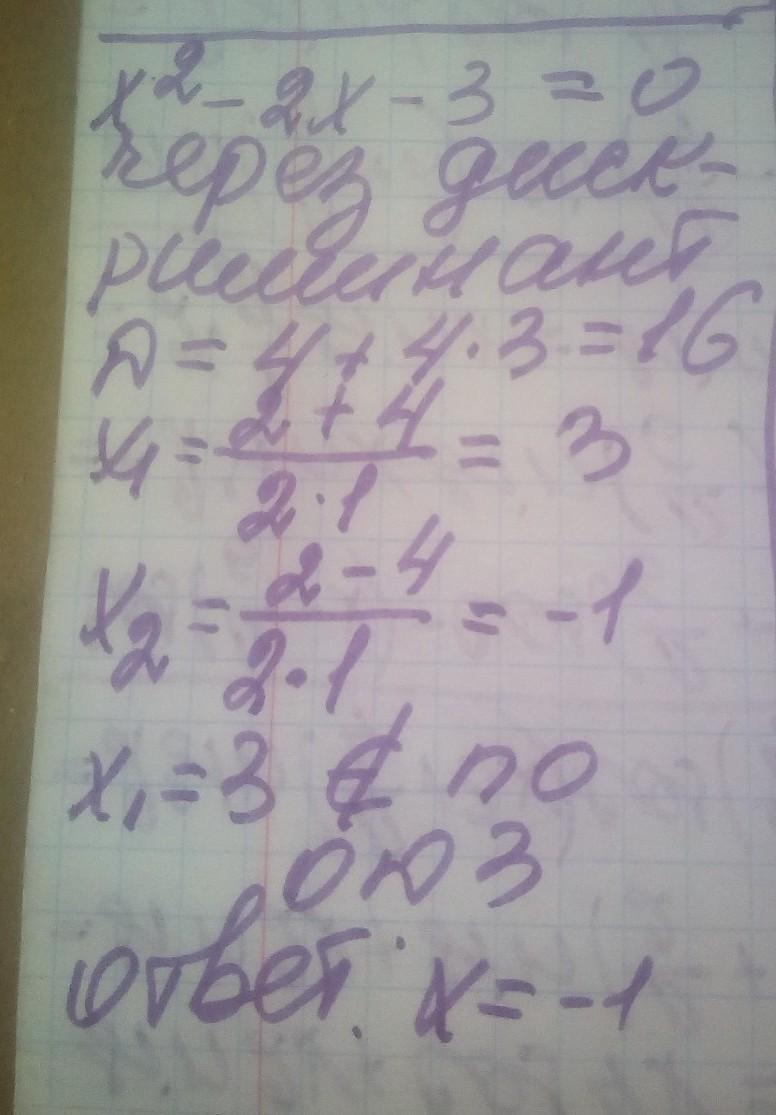
спасибо большое, а вы можете её через дискриминант решить?
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад