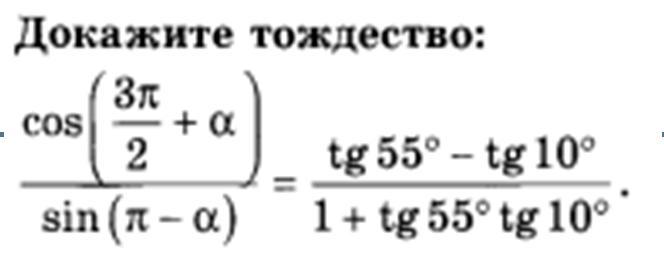Ответы
Ответ дал:
2
Ответ:
Рассмотрим левую часть:
Рассмотрим правую часть:
Получаем: 1 = 1
Объяснение:
используемые формулы:
последние две формулы - формулы приведения
fjorojodf:
Большое спасибо
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад