Question

Погомите пожалуйста, дам 20 баллов ​

Answer 1

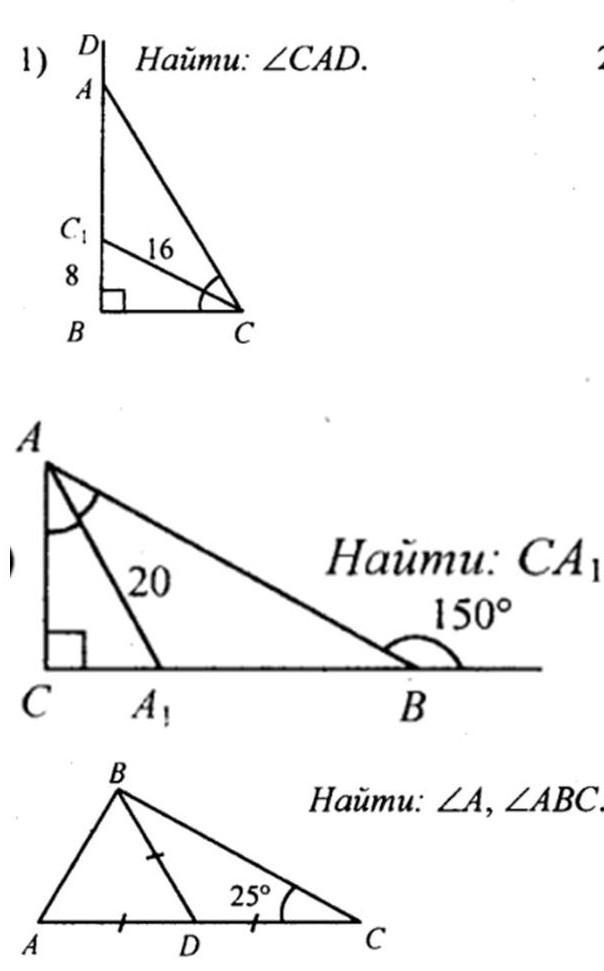
1)

САD=ABC+BCD

Рассмотрим прямоугольный треугольник BCC1

По теореме синусов: СС1/sinB=BC1/sinC

sinC=1/2, ВСС1=30°

Значит, BCD=60°

CAD=90°+60°=150°

2)

ВАС=150°-90°=60°

АА1- биссектриса, САА1=30°

Также по теореме синусов

АА1/sinC=CA1/sinA

CA1=10

3)

если медиана равна половине стороны, то треугольник прямоугольный и эта медиана проведена к гипотенузе

Значит, угол АВС=90°

угол А=180°-90°-25°=65°

Answer 2

Ответ:Номер 1

Если катет лежит против угла 30 градусов,то он в два раза меньше гипотенузы

Рассмотрим треугольник СВС1

Катет С1В в два раза меньше гипотенузы СС1,поэтому мы можем предположить,что против катета С1В лежит угол 30 градусов,т е

<С1СВ=30 градусов

<С1СВ=<С1СА=30 градусов-по условию задачи

Тогда угол С треугольника АВС равен

<С=30•2=60 градусов

Сумма всех углов треугольника АВС равна 180 градусов

<А=180-(90+60)=180-150=30 градусов

Угол А внутренний угол треугольника,угол САD-внешний угол,смежный с внутренним углом А

Внутренний угол и смежный ему внешний угол треугольника в сумме равны 180 градусов

<САD=180-30=150 градусов

Есть правило,что два внутренних угла не смежных с внешним в сумме составляют его градусную меру,так что на вопрос можно было бы ответить раньше

<САD=90+60=150 градусов

Номер 2

<А1ВА=180-150=30 градусов

<А=180-(90+30)=180-120=60 градусов

<САА1=<А1АВ=60:2=30 градусов-по условию задачи

<АА1В=180-(30+30)=180-60=120 градусов

<АА1С=180-(90+30)=180-120=60 градусов

Номер 3

Треугольник ВDC равнобедренный по условию задачи,поэтому углы при его основании равны

<DBC=<C=25 градусов

<ВDC=180-25•2=130 градусов

Угол АDB и угол DBC являются смежными углами,их сумма равна 180 градусов

<ADB=180-130=50 градусов

Треугольник АВD равнобедренный по условию задачи,угол АDB-угол при вершине,а углы при основании треугольника равны между собой

<АВD=<A=(180-50):2=130:2=65 градусов

Объяснение: